Equations as Functions
Equations that Define Relations
Suppose we have an equation in two variables x and y. Let’s
consider y = 4x + 3 and
x2 - y2 = 1.
For any equation, the solution set is the set of ordered pairs (x, y)
for which the equation holds true when the values are substituted
for x and y. Since a set of ordered pairs is a relation, we can
conclude that a solution set is a relation. In this way, equations
represent relations.
A relation that can be represented by an equation can easily be
visualized by graphing the equation. The graphs of y = 4x + 3 and
x2 - y2 = 1 are shown.
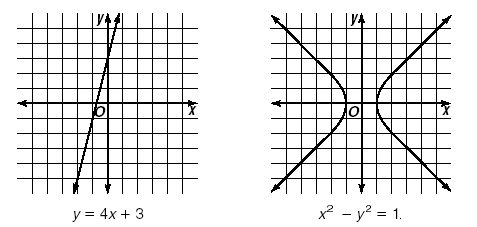
When is a Relation a Function?
The set of first coordinates in a relation is called the domain of the
relation. The set of second coordinates is called the range.
Remember that a relation is a function if each element of the
domain is paired with exactly one element in the range.
When we have a relation defined by an equation, we can graph the
equation and then visually determine whether or not it is a function
by using the vertical line test.
Key Idea
For a relation defined by an equation, the relation is a function if
every vertical line intersects the graph of the equation in at most
one point.
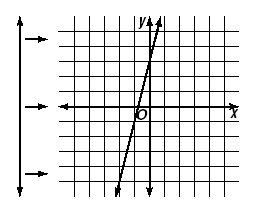
Consider the graph of y = 4x + 3. Using the vertical line test, we find
that the equation does define a function.
| As the vertical line moves to
the right across the graph, it
intersects only one point at a
time. |
 |
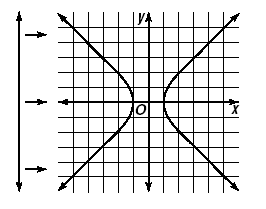
Consider the graph of
x2 - y2 = 1. Using the vertical line test, we
find that the equation does not define a function.
| As the vertical line moves to
the right across the graph, it
usually intersects the graph in
two points. Sometimes it does
not intersect the graph at all. |
 |
Recognizing Functions Algebraically
Another way to recognize when an equation defines a function is to
solve for y in terms of x.
Key Idea Any equation which has y on one side and a single formula
involving x on the other side defines a function.
The following equations are examples of functions.
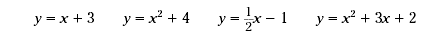
Some equations are not functions. Consider x2 - y2 = 1. If x2
- y2 = 1 is solved for y, the result is
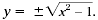 The symbol
± indicates
that there are two formulas on the right side of the equation for y.
Hence, x2 - y2 = 1 does not represent a function.
If an equation is not written in the form y = (formula in x), the
equation may still determine a function. Consider the following
example.
In 4x - 2y = 10, y is not isolated on the left side. However, we can
solve the equation for y.
| 4x - 2y 4x - 2y + 2x
-2y |
= 10 = 10 - 4x
= - 4x + 10 |
Subtract 4x from each side. |
 |
 |
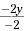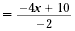Divide each side by -2. |
| y |
= 2x - 5 |
|
This is now in the form y = (formula in x) and gives a function.
Key Idea If, in an equation, we can solve for y as a single formula in terms
of x, then that equation represents a function.
Functions as Rules
Functions can also be thought of as rules that take an input value of x and
produce an output value of y. We often give these rules names such as f, g, h,
etc. We can then define a function by a formula in x.
The rule f(x) = x2 + 5 represents a function. We can think of it as a relation by taking the function
to be the set of all ordered pairs of the form (x, f(x)) = (x, x2 + 5). It is
also the solution set of y = x2 + 5.
Often we are given an equation in which y is not given as a formula
in x, but we can solve for y in terms of x to get a rule defining the
function.
In y + x = x2, we can solve for y by subtracting x from each side
to get
y = x2 - x.
This equation now gives a function. If we name the function f, then
the function is defined by
f(x) = x2 - x.
|
