Finding the Equation of an Inverse Function
The following procedure is helpful when trying to find the equation of the
inverse of a function.
Procedure —
To Find the Equation of the Inverse of a Function
If a function f(x) has an inverse, the following may be used to find
the inverse function f -1(x).
Step 1 Replace f(x) with y.
Step 2 Switch the variables y and x.
Step 3 Solve for y.
Step 4 Replace y with f -1(x).
Note:
Why do we switch x and y when finding an
inverse function?
This is because if the function f(x) is
satisfied by an ordered pair (a, b) then the
inverse function f -1(x) is satisfied by the
ordered pair (b, a).
Example
Given f(x) = 12x - 7, find f -1(x).
Solution
| Step 1 Step 2
Step 3 |
Replace f(x) with y.
Switch the variables y and x.
Solve for y.
Add 7 to both sides. |
y x
x + 7 |
= 12x - 7 = 12y - 7
= 12y |
| |
Divide both sides by 12.
|
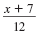 |
= y |
| |
We usually write y on the left. |
y |
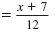 |
| Step 4 |
Replace y with f -1(x). |
f-1(x) |
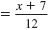 |
So, the inverse of f(x) = 12x - 7 is
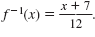
Note:
Notice that in f(x) = 12x - 7, the input is
multiplied by 12 and then 7 is subtracted
from that product.
The reverse is true for the inverse.
That is, in
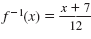 ,
7 is
added to the input and then that
sum is divided by 12. ,
7 is
added to the input and then that
sum is divided by 12.
|