Operating with Complex Numbers
Some equations have no real solutions. For instance, the quadratic equation
| x2 + 1 = 0 |
Equation with no real solution |
has no real solution because there is no real number x that can be squared to produce
-1. To overcome this deficiency, mathematicians created an expanded system of
numbers using the imaginary unit i, defined as
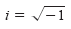 |
Imaginary unit |
where i2 = -1. By adding real numbers to real multiples of this imaginary unit, we
obtain the set of complex numbers. Each complex number can be written in the
standard form,
a + bi.
Definition of a Complex Number
For real numbers a and b, the number a + bi
is a complex number. If b ≠ 0, a + bi is called an
imaginary number, and bi
is called a pure imaginary number.
To add (or subtract) two complex numbers, you add (or subtract) the real and
imaginary parts of the numbers separately.
Addition and Subtraction of Complex Numbers
If a + bi and c + di are two complex numbers written in standard form, their
sum and difference are defined as follows.
Sum:
(a + bi) + (c + di) = (a + c) + (b + d)i
Difference: (a + bi) - (c + di) = (a - c) + (b - d)i
The additive identity in the complex number system is zero (the same as in the
real number system). Furthermore, the additive inverse of the complex number
a + bi
is
| -(a + bi) = -a - bi |
Additive inverse |
Thus, you have (a + bi) + (-a - bi) = 0 + 0i = 0.
Example 1
Adding and Subtracting Complex Numbers
| a. (3 - i) + (2 + 3i) |
= 3 - i + 2 + 3i |
Remove parentheses. |
| |
= 3 + 2 - i + 3i |
Group like terms. |
| |
= (3 + 2) + (- 1 + 3)i |
|
| |
= 5 + 2i |
Standard form |
| b. 2i + (-4 - 2i) |
= 2i - 4 -2i |
Remove parentheses.
|
| |
= -4 + 2i - 2i |
Group like terms. |
| |
= -4 |
Standard form |
|