Powers/Exponents and Operations

Integers = {..., -3, -2, -1, 0, 1, 2, 3, ...}

Addition Rules

Same signs: Add the absolute values and use the common sign.

Different signs: Subtract the lesser absolute value from the greater absolute value. Use the sign of the number with the greater absolute value.

Subtraction Rule

To subtract an integer, add its opposite.

Multiplication and Division Rules

Same signs: The product/quotient is positive. Different signs: The product/quotient is negative.

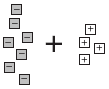matches -3

“The gray squares represent negative integers and the white squares represent positive integers. has a greater absolute value, so the answer is negative. And so the answer is ”

Warm-Up

2 - (-3 ) matches 5.

“When you add the opposite, you have 2 + 3 = 5.”

Warm-Up

3(-4) matches -12

“The signs are different, so the answer will be negative. Because 3 × 4= 12, the answer is -12.”

An exponent represents the number of times a base is used as a factor. An exponent of 2 is the second power; an exponent of 3 is the third power.

In the expression -3², only the 3 is raised to a power, so -3² = -9.

The expression (-3)² = (-3)(-3) = 9.

-5² matches -25.

“Only the 5 is being squared, so the answer is -25.”

You use order of operations to evaluate an expression that has more than one operation:

1. Evaluate expressions inside grouping symbols.

2. Evaluate powers.

3. Multiply and divide from left to right.

4. Add and subtract from left to right.

-8 - (-6) + 4 matches 2.

“Subtraction is done first, so -8 - (-6) is -8 + 6, which equals -2. Then add -2 + 4, which is 2.”

5(6 + 8) matches 5(6) + 5(8).

“Distribute the 5, and the answer is 5 times 6 plus 5 times 8.”

a(b + c) = ab + ac

a(b - c) = ab - ac

6(8 + 5) = 6(8) + 6(5)

7(9 - 4) = 7(9) - 7(4)