Simplifying Complex Fractions

Before introducing the definition of complex fraction, let's remember:

• A simple fraction is a fraction containing no other fractions as part of its numerator or its denominator.
• A simple fraction can be simplified. What we intend to do when simplifying a simple fraction is to obtain an equivalent fraction that looks simpler (i.e. it has less terms in its numerator and denominator).

Now that we have this clear, we can learn that

• complex fractions are fractions whose numerator and/or denominator themselves are expressions containing other fractions.
• A complex fraction can also be simplfied. What we mean by simplifying a complex fraction is to rearrange it into an equivalent simple fraction which is in simplest form.

You should already know how to simplify a simple fraction. But, how do we simplify a complex fraction?

When the numerator and denominator of a complex fraction are just single simple fractions themselves, simplifying it turns out to be very easy. We just use the wellknown “invert and multiply” rule: multiply the fraction in the numerator by the reciprocal of the fraction in the denominator:

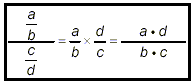
We have turned the initial complex fraction on the left into a single simple fraction on the right. After you have done this, all that is left is to check whether the simple fraction on the right can be simplified any further.

Be careful, because this step is justified only if the numerator and denominator of the original complex fraction are both single simple fractions.

Example 1:

Simplify: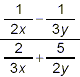

solution:

The strategy illustrated in the previous examples is easily applied to this complex fraction. First, the numerator can be simplified to give

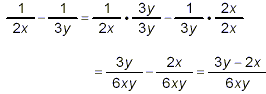
The denominator can be simplified to give

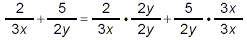
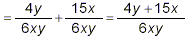
Substituting these simplified expressions back into the original complex fraction then gives

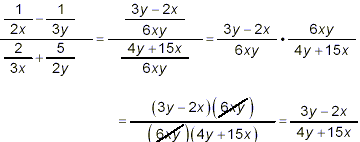
after cancelling common factors in the resulting numerator and denominator. Since no further factorization is possible in either the numerator or the denominator of this fraction, and since no common factors still exist that can be cancelled between the numerator and denominator of this last expression, it must be the required most simplified form of the original complex fraction.

Example 2:

Simplify: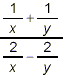

solution:

You can use this example as a practice problem. Try carrying out the required simplification first before you look at the outline of the solution that follows. This example has essentially the same structure as that of Example 1 above. So, first simplify the numerator

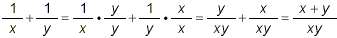
Then, simplify the denominator:

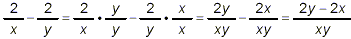
So

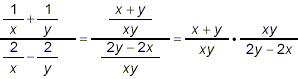
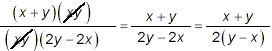
The numerator and denominator of this last expression are both fully factored and there are no common factors in them which can be cancelled. So this last fraction must be the required simplified form of the original complex fraction.