Solving Inequalities with Fractions and Parentheses
After studying this lesson, you will be able to:
- Solve inequalities with fractions and parentheses.
Below are the steps for solving inequalities. Remember we are
applying the same rules as we did for equations. If an inequality
contains fractions, the fractions can be cleared out by
multiplying every term in the inequality by the common
denominator. Also, if an inequality contains parentheses, the
parentheses can be removed by using the distributive property.
If we multiply or divide an inequality by a negative, we
reverse the inequality symbol.
The steps for solving inequalities are the same as those for
solving equations:
1. Remove parentheses and clear fractions (if necessary)
2. Collect like terms on each side of the inequality symbol
3. Get the variables together on one side
4. Isolate the variable
5. Check
Example 1
| -6 < 5y - (2y - 9) |
We need to distribute to remove the
parentheses Since there is a negative in front of the
parentheses, we distribute a negative 1. |
| -6 < 5y -2y + 9 |
We get this after distributing a -1 |
| -6 < 3y + 9 |
Add like terms |
| -6 - 9 < 3y + 9 - 9 |
Subtract 9 from each side |
| -15 < 3y |
Divide each side by 3 |
| -5 < y |
|
Check by substituting into the original inequality
Example 2
| 3 (3x + 6 ) < 3 ( 6x - 9
) |
Remove parentheses by multiplying |
| 9x + 18 < 18x - 27 |
Now, we need to get the variables
together |
| 9x + 18 - 9x < 18x - 27 -
9x |
Subtract 9x from each side |
| 18 < 9x - 27 |
|
| 18 + 27 < 9x - 27 + 27 |
Add 27 to each side |
| 45 < 9x |
Divide each side by 9 |
| 5 < x |
|
Check by substituting into the original inequality
Example 3
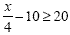 |
|
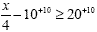 |
Add 10 to each side |
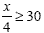 |
Now we need to clear the fraction |
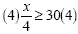 |
Multiply each side by the common
denominator (4) |
x 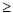 120 120 |
|
Check by substituting into the original inequality
|