Writing Numbers in Scientific Notation

There are two steps to writing a large positive number in scientific notation. Consider the number 1,649,000,000. The first step is to move the decimal point to the right of the leftmost digit. Remove all of the zeros on the far right.

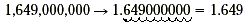
The second step is to multiply this number by a power of 10. To find the power of 10, count the number of places you moved the decimal point.

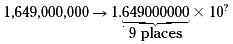
So, in scientific notation, 1,649,000,000 is written 1.649 ×10 ⁹.

Example 1

Write 3,587,000,000,000 in scientific notation.

Solution

3,587,000,000,000 = 3.587 ×10 ¹² Move the decimal point 12 places to the left. Multiply by 10 ¹².

To write numbers less than 1 in scientific notation, there is a similar method. Consider the number 0.0000387. The first step is to move the decimal point to the right of the first nonzero digit. Remove all of the zeros on the far left.

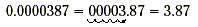
The second step is to multiply this number by a power of 10. To find the power of 10, count the number of places you moved the decimal point. Then use the negative of that number as the exponent of 10.

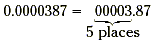
In this case, the decimal point was moved 5 places. So, -5 will be used as the exponent of ten. In scientific notation, 0.0000387 is written 3.87 ×10 ^-5.

Example 2

Write 0.000000634 in scientific notation.

Solution

0.000000634 = 6.34 ×10 ^-7 Move the decimal point 7 places to the right. Multiply by 10 ^-7.

Comparing and Ordering Numbers in Scientific Notation

It is easy to compare two numbers that are given in scientific notation.

Key Idea

To compare two numbers given in scientific notation, first compare the exponents. The one with the greater exponent will be greater. If the exponent is the same, compare the two numbers that are being multiplied by comparing their decimals.

Example 3

Compare 6.23 × 10 ¹⁴ and 8.912 × 10 ¹² .

Solution

Since the exponent in the first number is greater than the exponent in the second number, 6.23 × 10 ¹⁴ is greater than 8.912 × 10 ¹².

Example 4

Which is greater, 5.15 × 10 ^-4 or 6.35 × 10 ^-5 ?

Solution

Since -4 is greater than -5, 5.15 × 10 ^-4 is greater than 6.35 × 10 ^-5 .

Example 5

Compare 3.28 × 10 ¹⁷ and 4.25 × 10 ¹⁷ .

Solution

The exponents are both 17. So, we need to compare the numbers that are being multiplied. Since 4.25 is greater than 3.28, 4.25 × 10 ¹⁷ is greater than 3.28 × 10 ¹⁷ .