Negative and fractional powers
Introduction
Sometimes it is useful to use negative and fractional powers.
These are explained on this leaflet.
1. Negative powers
Sometimes you will meet a number raised to a negative power.
This is interpreted as follows:
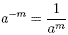
This can be rearranged into the alternative form:
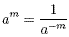
Example
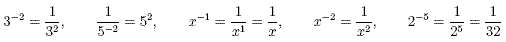
Exercises
1. Write the following using only positive powers:
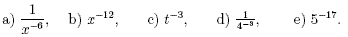
2. Without using a calculator evaluate 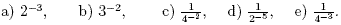
Answers
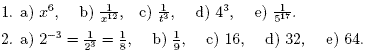
2. Fractional powers
To understand fractional powers you first need to have an
understanding of roots, and in particular square roots and cube
roots.
When a number is raised to a fractional power this is
interpreted as follows:
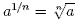
So,
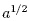 is a square root of a
is a square root of a
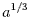 is the cube root of a is the cube root of a
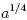 is a fourth root of a is a fourth root of a
Example
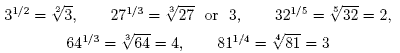
Fractional powers are useful when we need to calculate roots
using a scientific calculator. For example to find 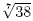 we
rewrite this as we
rewrite this as 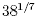 which can be evaluated using a scientific
calculator. You may need to check your calculator manual to find
the precise way of doing this, probably with the buttons which can be evaluated using a scientific
calculator. You may need to check your calculator manual to find
the precise way of doing this, probably with the buttons 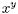 or or 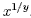
Check that you are using your calculator correctly by
confirming that 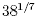 = 1.6814 (4 dp) = 1.6814 (4 dp)
More generally 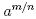 means means 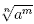 or
equivalently or
equivalently 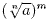
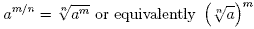
Example
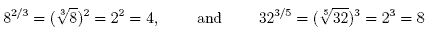
Exercises
1. Use a calculator to find 
2. Without using a calculator, evaluate 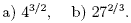
3. Use the third law of indices to show that
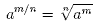
and equivalently
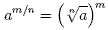
Answers
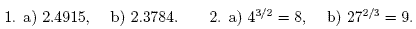
|