Raising a Quotient to a Power
Consider an example of applying known rules to a power of a quotient:
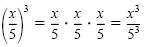
We get a similar result with a negative power:
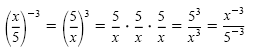
In each of these cases the original exponent applies to both the numerator and
denominator. These examples illustrate the power of a quotient rule.
Power of a Quotient Rule
If a and b are nonzero real numbers and n is any integer, then
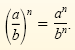
Example 1
Using the power of a quotient rule
Use the rules of exponents to simplify each expression. Write your answers with
positive exponents only. Assume the variables are nonzero real numbers.

Solution
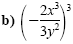 |
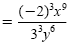 |
Because (x3)3 = x9 and (y2)3
= y6 |
| |
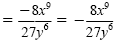 |
|
A fraction to a negative power can be simplified by using the power of a quotient
rule as in Example 3. Another method is to find the reciprocal of the fraction first, then
use the power of a quotient rule as shown in the next example.
Example 2
Negative powers of fractions
Simplify. Assume the variables are nonzero real numbers and write the answers
with positive exponents only.
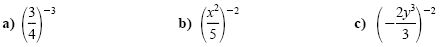
Solution
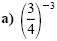 |
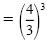 |
The reciprocal of
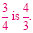 |
| |
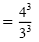 |
Power of a quotient rule |
| |
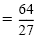 |
|
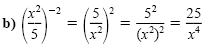
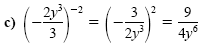
|