Simplifying Square Roots That Contain Whole
Numbers
To make it easier to work with an algebraic expression, we often
simplify it.
For example, you have simplified expressions as follows:
• 5(x - 4) + 2x = 7x - 20
•
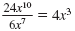
To simplify a square-root radical, we examine the factors of the radicand.
If any of those factors are perfect squares, we rewrite the radical so there
are no perfect square factors under the radical sign.
To do this, we use the Multiplication Property of Square Roots.
We will learn two methods for simplifying square-root radicals.
To see how each method works, let’s s simplify
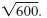
• Method 1 Use Perfect Square Factors
Identify perfect square factors of 600.
The numbers 4, 25, and 100 are each perfect square factors of 600.
Using those factors, we can write
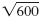 in several ways: in several ways:
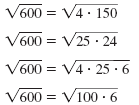
| The factorization 100 · 6 contains
100, the largest perfect square that is
a factor of 600. So we use that form. |
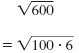 |
Use the Multiplication Property of
Square Roots to write
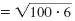 as the product of two radicals. as the product of two radicals. |
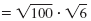 |
Simplify
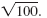 |
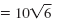 |
Thus, in simplified form,
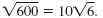
Note:
Here is another way to use perfect squares
to simplify
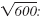
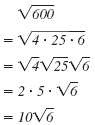
| • Method 2 Use Prime Factors |
|
| If you have trouble finding a perfect
square factor of the radicand, write
its prime factorization. Then, group
the factors to form perfect squares. |
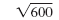 |
| Write the prime factorization of 600. |
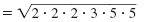 |
| Group pairs of factors to form perfect
squares. |
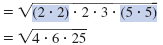 |
| Write as a product of three radicals. |
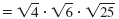 |
Simplify
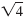 and simplify and simplify
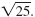 |
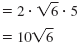 |
Thus, in simplified form,
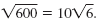
|