Arithmetics
These are the only rules that we need in order to develop
arithmetic/algebra.
If you cannot figure out how to justify an algebraic statement
directly from these rules, then it is probably false!
Addition is (has):
Commutative a + b = b + a
Associative ( a + b ) + c = a + ( b + c )
Unital a + 0 = a
Inverses a + ( - a ) = 0
Subtraction as inverse operation If a + b = c , then a = c - b
and b = c - a .
Multiplication is (has):
Commutative ab = ba
Associative ( ab ) c = a ( bc )
Unital a 1 = a
Inverses 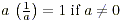
Division as inverse operation If ab = c with
a 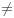 0
and b 0
and b 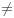 0 then 0 then 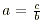 and and 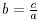 . .
Multiplication by Zero Law a 0 = 0
Zero Factor Law If ab = 0, then a = 0 or b =
0.
Combining the two operations we have the
Distributive Law a ( b + c ) = ab + ac and
its cousin
Distributing over Negatives a ( b - c ) = ab
- ac
Remember, the Zero Factor Law is very important since it lets
us find roots of polynomials (or more general functions) by
factoring.
|