Fractions
The aim of this document is to provide a short, self
assessment programme for students who wish to acquire a basic
competence in the use of fractions.
The first thing to note is that all fractions can be
represented in many different ways. Thus 3/12, 4/16, 5/20
represent the same fraction which, in its lowest terms , is 1/4.
Example 1
To show that each of the above fractions is equal to 1/4 we
proceed as follows:
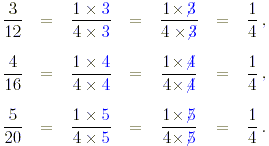
The fractions in the left hand column each have a factor
common to the numerator (top) and denominator (bottom) of that
fraction, which is cancelled to give the fraction in its lowest
terms.
In many problems it is necessary to carry out the reverse
procedure, i.e. multiplying the numerator and denominator of a
fraction by a common factor to obtain an equivalent fraction.
Example 2
Arrange each of the following fractions in the order of size.
( a ) 3 /4 , ( b ) 2 /3 , ( c ) 5 /6 .
Solution
To determine their relative order, each fraction must be
written with the same denominator. The smallest such number is
12.
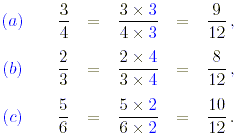
The order of size, starting with the smallest, is 2/3, 3/4,
5/6.
Exercise
In each case below, arrange the fractions in increasing order
of size.
(a) 7/12 , 1/2 , 2/3 .
(b) 1/3, 5/8, 3/4 .
(c) 5/6, 8/9, 11/12.
(d) 2/3, 3/5, 7/10.
Solution
(a) The least common denominator of the
fractions is 12, so
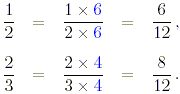
Since 7/12 already has 12 as denominator, the required order
of the fractions is
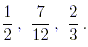
(b) In this case, the least common
denominator of the fractions is 24.
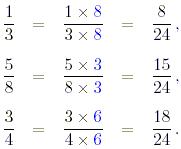
The fractions are thus increasing in the order in which they
appear.
(c) In this case the least common denominator
of the fractions is 36.
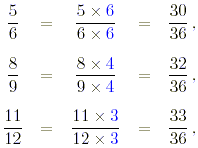
The fractions are thus increasing in the order in which they
appear.
(d) In this case the least common denominator
of the fractions is 30.
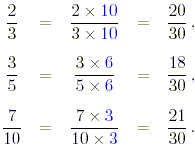
The fractions, in increasing order of size, are 3/5, 2/3,
7/10.
Now try this short quiz.
Quiz
Of the following sets of fractions, exactly one is in
ascending order of size. Which one?
(a) 1/3, 3/5, 5/8. (b) 3/8, 2/3, 3/4. (c) 2/3, 3/4, 1/2. (d)
3/5, 5/7, 1/2.
Solution
Putting each of them in the form of a fraction with
denominator 24,
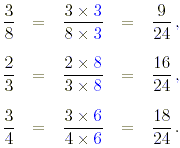
These are obviously in ascending order. Repeating this with
the others will show that this is the only set in ascending
order.
|