Solving Linear Inequalities
Solving a linear inequality means writing it in a form so that
only y appears on the left-hand side, and only x and constants
appear on the right side. This is similar to solving an equation
for y. It is easy to graph the solution sets for linear
inequalities. Simply graph the corresponding boundary line and
then shade the region either above or below the line.
Solving linear inequalities can be done by using the Addition
and Multiplication Properties of Inequalities, just as the
corresponding properties of equations are used to solve linear
equations. This is best illustrated by examples.
Example 1
Solve y + 7 < 2 x + 5.
Solution
First, rewrite the inequality so that y is on the left-hand
side by itself.
| y + 7 < |
2 x + 5 |
Subtract 7 from each side. |
| y < |
2 x - 2 |
|
So, the solution set is the set of all points that lie below
the line y = 2x - 2, as shown in the graph below.
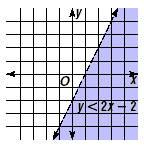
Notice that there is a dashed line on the boundary, since the
inequality symbol is < , not 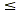 . .
Example 2
Solve 2y 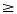 x + 6. x + 6.
Solution
To solve the inequality, first divide each side by 2 to
isolate the y .
2y 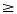 |
x + 6 |
|
y 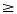 |
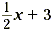 |
Divide each side by 2. |
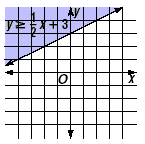
The solution set is the set of points on and above the line 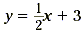 , as shown in the graph
below , as shown in the graph
below
Example 3
Solve 3 - y 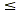 x + 5. x + 5.
Solution
First, use the properties of inequalities to isolate the y.
3 - y 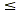 |
x + 5 |
|
- y 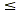 |
x + 2 |
Subtract 3 from each side. |
y 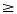 |
- x - 2 |
Multiply each side by -1. Reverse the
inequality symbol. |
The graph of y 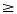 x - 2 is shown below. x - 2 is shown below.
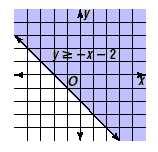
Notice that a solid line is on the boundary of the region.
Recall that the Multiplication Property of Inequalities states
that multiplying each side of an inequality by the same positive
number produces an equivalent inequality. However, when
multiplying each side by the same negative number, the inequality
symbol must be reversed to get an equivalent inequality.
|