Solutions to Linear Equations in Two Variables
1. Given 2x − 3y = 6 build the table for using an arithmetic sequence as replacement values.
→ Logically, we know that it is easy to plot ordered pairs if
both coordinates are integers.
In this equation we note that all of the numbers except the y-coefficient are
even integers.
From arithmetic we know that:
| Multiplying by any even integer will yield
an even integer as the product
and
Adding two even integers will result in
an even integer as the sum.
|
Even × Odd (or Even) = Even
Even ± Even = Even |
Now if we choose an even integer as the replacement for the y- value then the resulting x-value
will be an integer. Therefore, we put the "sequence of even integers" in the table for y
then complete the computation below for each y-value and put each corresponding
x-value in
the table. Repeat the process for the other y-values to find the resulting
x-values. Note any
sequences and write the common differences.
| 2x − 3y = 6
Let y = - 4: 2x − 3(- 4) = 6,
repeat for the other numbers
y = - 2: 2x − 3(- 2) = 6,
y = 0: 2x − 3( 0 ) = 6,
y = 2: 2x − 3( 2 ) = 6,
y = 4: 2x − 3( 4 ) = 6, |
x = - 3
x = 0
x = 3
x = 6
x = 9 |
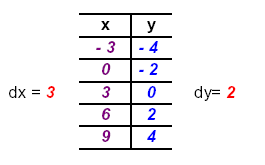 Check to see that
both columns of values are arithmetic sequences.
|
For the point (- 3, - 4) replace x = - 3 and y = - 4 in the given equation 2x − 3y = 6
CHECK:
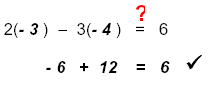
For the point (9, 4) replace x = 9 and y = 4 in the given equation 2x − 3y = 6
CHECK:
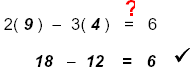
You should always form the practice of checking all of your work whenever
you can.
2. Graph 2x + 3y = 7. Build a table for 2x + 3y = 7.
Again let us turn to LOGIC: We know that for integers:
| Odd × Odd = Odd
Odd ± Odd = Even |
Even × Odd (or Even) = Even Even ± Odd = Odd |
In order to keep both coordinates as integers choose the replacement
values for the y to be odd integers. We choose the sequence of odd integers for
replacement for y- values and the resulting x-sequence will be integers. Complete the
computation below and put the number in the table. Repeat the process for the other y-values to
find the resulting x-values.
| 2x + 3y = 7 Let y = 1
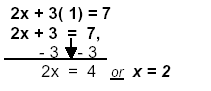
repeat for the other numbers
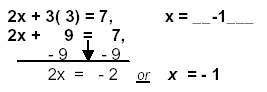 |
Put these values in
the table, then write
the “common
differences†for both
x and y.
Use the value for dx
to complete the table
values for x.
|
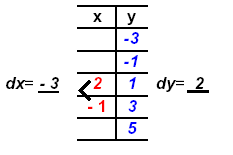
For complete table see below. |
| Note adding ± 3 to given values forms an arithmetic sequence.
To be sure you should always check the “outer pointsâ€.
|
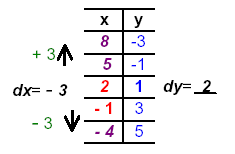 |
Check:
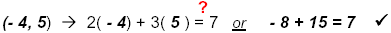
Check:
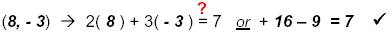
Check the dy and dx on your table.
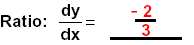
|