The Quadratic Formula
It is possible to find the solutions of a quadratic equation without having to graph and use
a calculator, without having to factor and without having to complete the square. The
key to being able to find the solutions of a quadratic equation is a relationship called the
quadratic formula.
The values of x that solve the quadratic equation:
a · x2 + b · x + c = 0,
are:
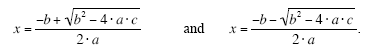
Because of the similarity in the two formulas, they are often combined (by writing “±†in
place of the “+†and “-â€) into a single formula that is known as the quadratic formula:
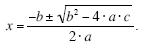
Example
Find all of the solutions of the following quadratic equation:
x2 + 8 · x - 20 = 0.
Solution
In this equation, the values of the coefficients a, b and c are:
a = 1
b = 8
c = -20.
Plugging these values into the first version of the quadratic equation (the version with the
“+†in it) gives:
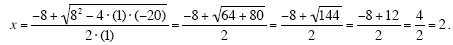
Plugging these values into the second version of the quadratic equation (the version with
the “-†in it) gives:
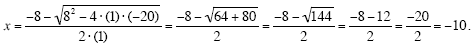
There are two solutions of the quadratic equation x2 + 8
· x - 20 = 0, and they are x = 2
and x = -10.
Order of Operations and the Quadratic Formula
The quadratic formula:
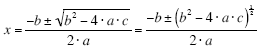
is the most complicated formula that we have done in the course so far. This formula
involves parentheses, exponents, multiplication, division, addition and subtraction.
When you use the quadratic formula to find the solutions of a quadratic equation you
have to pay attention to the order of operations to ensure that you evaluate the formula
correctly.
This principle of working out the power (or exponent) first, and leaving the multiplication
until you have finished the power (or exponent) is part of a system of rules for evaluating
complicated equations. The rules are called the Order of Operations.
• B: Work out everything in brackets/parentheses first.
• E: Next, work out all of the exponents.
• M/D: When you have finished with the exponents, do all of the multiplication and
division.
• A/S: Finally, do all of the addition and subtraction.
Some people use a mnemonic device to remember the order that the operations:
| Parentheses |
Please |
| Exponents |
Excuse
|
| Multiplication |
My |
| Division |
Dear |
| Addition |
Aunt |
| Subtraction |
Sally.
|
This applies to the quadratic formula by stipulating that you should evaluate the quadratic
formula in the following order:
• First: Work out b2 - 4"a"c first.
• Second: Take the square root of b2 - 4
· a · c.
• Third: Add or subtract this square root from -b.
• Fourth: Divide by 2 · a.
|