Exponents and Their Properties
Recall:
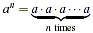 if n is a positive
integer.
New Stuff:
When you have a product of two terms with the same base, the
exponents add together.
Rule (The Product Rule)
For any number a and positive integers m and n , a m
a n = a m + n.
- Multiplication of powers leads to addition of the
exponents. When you raise something to a power, you are
really multiplying it by itself several times. Thus, if
you raise a power to a power, you should add the exponent
to itself several times. In other words, multiply the
powers.
Rule (Power Rule)
For any number a and any positive integers m and n , ( a
m ) n .
- Since multiplication leads to addition of exponents, it
makes sense that division would lead to subtraction.
Rule (The Quotient Rule)
For any number a ( a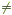 
0) and any positive integers m and n for which m > n , .
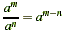The quotient rule allows us to determine what a 0 exponent
should mean. Suppose that we allow m = n in the rule above. Then
we have 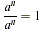 (since the top and
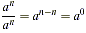bottom are the same). But we also have  . Thus, we should define a 0 =
1.
Definition ( 0 as an Exponent)
For any real number a , a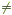
0, a 0 = 1.
- That this is a good way to define 0 as an exponent is
verified by looking at how well this works with the other
rules.
The multiplication rule: If this is a good
definition, then a n · a 0 should be the
same as a n · 1. Indeed, it is, since a n
· a 0 = a n + 0 = a n and a
n · 1 = a n .
The power rule: The power rule is really just
an extension of the multiplication rule, so the definition works
with the power rule.
The quotient rule: We made the definition
specifically so it works with the quotient rule, so this works
too.
|
