Simplifying fractions
Introduction
Fractions involving symbols occur very frequently in
engineering mathematics. It is necessary to be able to simplify
these and rewrite them in different but equivalent forms. On this
leaflet we revise how these processes are carried out.
1. Expressing a fraction in its simplest form
An algebraic fraction can always be expressed in different,
yet equivalent forms. A fraction is expressed in its simplest
form by cancelling any factors which are common to both the
numerator and the denominator. You need to remember that factors
are multiplied together. For example, the two fractions 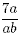 and and 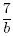 are equivalent. Note that there is a
common factor of a in the numerator and the denominator of are equivalent. Note that there is a
common factor of a in the numerator and the denominator of 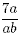 which can be cancelled to give which can be cancelled to give 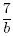 . .
To express a fraction in its simplest form,an y factors which
are common to both the numerator and the denominator are
cancelled.
Notice that cancelling is equivalent to dividing the top and
the bottom by the common factor. It is also important to note
that 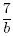 can be converted back to the equivalent fraction can be converted back to the equivalent fraction 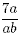 by multiplying both the numerator and denominator of by multiplying both the numerator and denominator of
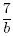 by a. by a.
A fraction is expressed in an equivalent form by multiplying
both top and bottom by the same quantity,or dividing top and
bottom by the same quantity
Example
The two fractions
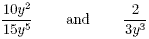
are equivalent. Note that
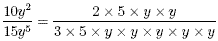
and so there are common factors of 5 and y × y . These can be
cancelled to leave 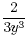 . .
Example
The fractions
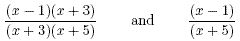
are equivalent. In the first fraction,the common factor ( x +
3) can be cancelled.
Example
The fractions
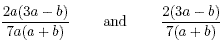
are equivalent. In the first fraction,the common factor a can
be cancelled. Nothing else can be cancelled.
Example
In the fraction
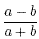
there are no common factors which can be cancelled. Neither a
nor b is a factor of the numerator. Neither a nor b is a factor
of the denominator.
Example
Express 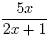 as an equivalent fraction with
denominator (2 x + 1)( x - 7). as an equivalent fraction with
denominator (2 x + 1)( x - 7).
Solution
To achieve the required denominator we must multiply both top
and bottom by ( x - 7). That is
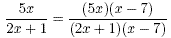
If we wished,the brackets could now be removed to write the
fraction as
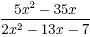
Exercises
1. Express each of the following fractions in its simplest
form:
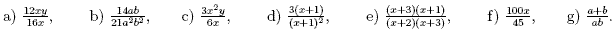
Answers
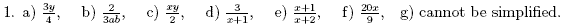
Whilst both a and b are factors of the denominator, neither a
nor b is a factor of the numerator.
|