Roots and Radicals: Solving Power Equations Algebraically
Solving a Power Equation
The objective of solving a power equation such as:
1.0725 · x0.808 =10,
is to find the numerical value of x that works in this equation.
Solving a Power Equation Using Algebra
You can also solve power equations using algebra, and although the manipulations for
solving power equations are not as straightforward as the manipulations for solving linear
equations, using algebra is often easier than using the calculator.
In order to use algebra to solve a power equation, you need to be able to use one of the
Laws of Exponents:
(x p )q = x p·q (Multiply the exponents.)
Locating the Intersection of Power Functions
When you were working with linear functions, one of the things that you learned how to
calculate was the x- and y-coordinates of the point (the intersection point) where the
graphs of two linear functions met.
Power functions also intersect, and you can find the x- and y-coordinates of the
intersection point using both a graphing calculator and algebra. In order to use algebra to
calculate the x-coordinate of the point where two power functions meet, you have to use
two of the Laws of Exponents:
(x p )q = x p·q (Multiply the exponents.)
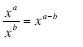 (Subtract exponents.) (Subtract exponents.)
Example:
Locating the Intersection Point of Power Functions Using Algebra
Find the x- and y-coordinates of the intersection point of the two power functions:
y =100· x-2 and
y = 6.25 · x2.
Solution
100 · x-2 = 6.25 · x2 (Set the two equations equal.)
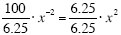 (Divide both sides by 6.25.) (Divide both sides by 6.25.)
16 · x-2 = x2 (Simplify both sides.)
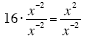 (Divide both sides by x-2.) (Divide both sides by x-2.)
16 · x-2-(-2) = x2-(-2) (Simplify the fractions with Law of Exponents.)
16 = x4 (Simplify both sides.)
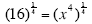 (Take the
14 power of both sides.) (Take the
14 power of both sides.)
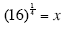 (Simplify with the Law of Exponents.) (Simplify with the Law of Exponents.)
x = 2 (Work out the rest on a calculator.)
To work out the y-coordinate, you can plug x = 2 into either of the power equations given
in the problem.
y =100 · (2)-2 = 25.
Radical Notation
An alternative notation, called radical notation, is sometimes used when writing
algebraic expressions and formulas that include fractional powers.
For example, a fractional power such as:
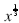 , ,
is sometimes written as:
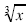 . .
A fractional power such as:
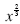 , ,
would be written in radical notation as:
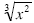 . .
If you are ever given an algebraic expression or formula expressed using radical
notation, it is best to convert the radicals to fractional powers and then simplify them as
much as possible using the laws of exponents. If you have to express your answer in
radical notation, then you can convert the answer back to radical notation when you have
completed all of your simplifications and manipulations.
|