Solving Inequalities
A real number a is a solution of an inequality if the inequality is
satisfied (is true) when a is substituted for x. The set of all solutions is
the solution set of the inequality.
Example 1
Solving an Inequality
Solve 2x - 5 < 7.
Solution
| 2x - 5 |
< 7 |
Original inequality |
| 2x - 5 + 5 |
< 7 + 5 |
Add 5 to both sides. |
| 2x |
< 12 |
Simplify. |
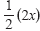 |
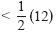 |
Multiply both sides by
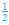 |
| x |
< 6 |
Simplify. |
The solution set is (-∞, 6).
NOTE In Example 1, all five inequalities listed as steps in the solution are called
equivalent
because they have the same solution set.
Once you have solved an inequality, check some x-values in your solution set to
verify that they satisfy the original inequality. You should also check some values
outside your solution set to verify that they do not satisfy the inequality. For example,
the figure below shows that whenx = 0 or x = 5 the inequality 2x - 5 < 7 is satisfied,
but when x = 7 the inequality 2x - 5 < 7 is not satisfied.
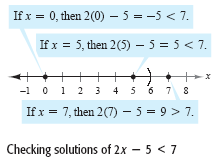
Example 2
Solving a Double Inequality
Solve -3 ≤ 2 - 5x ≤ 12.
Solution
| -3 ≤ |
2 - 5x |
≤ 12 |
Original inequality |
| -3 - 2 ≤ |
2 - 5x - 2 |
≤ 12 - 2 |
Subtract 2. |
| -5 ≤ |
- 5x |
≤ 10 |
Simplify. |
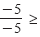 |
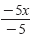 |
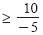 |
Divide by -5 and reverse both inequalities. |
| 1 ≥
|
x |
≥ -2 |
Simplify. |
The solution set is [-2, 1], as shown in the figure below.
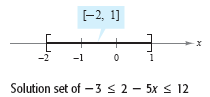
The inequalities in Examples 1 and 2 are linear inequalities—that is, they
involve first-degree polynomials.
|