Simplifying Complex Fractions

There are some fractions whose numerator and/or denominator themselves are expressions containing other fractions. We call these fractions complex fractions.

We already know one meaning of "simplifying fractions". That is, taking a simple fraction (i.e. a fraction that contains no other fractions neither in its numerator nor in its denominator) and manipulate it in order to get an equivalent algebraic form which has less terms in its numerator and denominator. However, when we talk about simplifying a complex fraction what we want to do is to rearrange the given complex fraction into an equivalent simple fraction which is in simplest form. (Note that by the phrase simple fraction, we mean a fraction which does not contain any other fractions in its numerator or in its denominator.)

There is one case where simplifying a complex fraction is very straightforward:

when the numerator and denominator of a complex fraction are just single simple fractions themselves.

Therefore, for the first step in simplifying the complex fraction, we just use the wellknown “invert and multiply” rule: multiply the fraction in the numerator by the reciprocal of the fraction in the denominator:

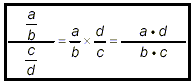
As you can see, the initial complex fraction on the left has been turned into a single simple fraction on the right. This step is justified only if the numerator and denominator of the original complex fraction are both single simple fractions. When the pattern in the box above is valid, all that is left to do in simplifying the original complex fraction is to use methods to check whether the simple fraction on the right can be simplified any further.

Example 1:

Simplify: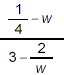

solution:

This is a complex fraction in which both numerator and denominator contain fractions. So we begin by simplifying each part into fully factored single simple fractions. For the numerator, we get

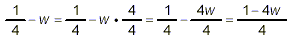
For the denominator, we get

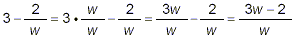
So now, getting back to the original fraction, we have

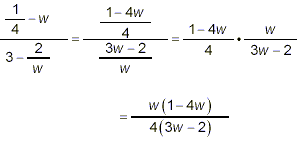
Since neither numerator nor denominator of this last form can be factored further, and since there are no common factors that can be cancelled here between the numerator and the denominator, this is as much as the original fraction can be simplified and so this last form must be the required final answer.

Example 5:

Simplify: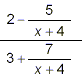

solution:

This is a complex fraction similar in form to the one in Example 1. The fact that the denominators in the fractions found in the numerator and denominator of this complex fraction are binomials does not change the overall strategy of simplification here. We still start by reducing the expressions in the numerator and denominator of the complex fraction to fully factored single simple fractions. For the numerator this gives

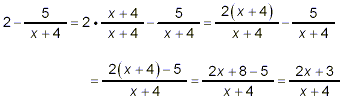
For the denominator, we get

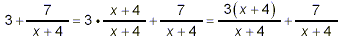
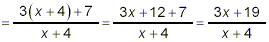
Substituting these two simplified forms for the numerator and denominator, respectively, of the original complex fraction then gives

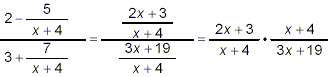
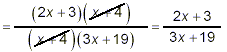
as the final simplified form. We know we are done here because:

• this is a single simple fraction (no other fractions are present in either its numerator or its denominator)
• this simple fraction cannot be simplified further because the numerator and denominator cannot be factored further and there are no common factors present in the two parts which can be cancelled.