Extraneous Solutions
If an equation contains a variable in the denominator of a rational
expression, then it is possible that the equation may not have a solution.
| For example, let’s try
to solve this equation:
|
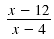 |
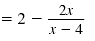 |
| Multiply both sides
by (x - 4). |
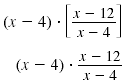 |
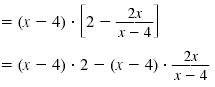 |
| Cancel. |
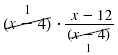 |
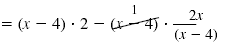 |
| Distribute the 2.
Simplify the right side.
Add 12 to both sides. |
x - 12 x - 12
x - 12
x |
= (x - 4) · 2 - 2x
= 2x - 8 - 2x
= -8
= 4 |
| The result is x = 4.
However, notice what happens when we check the solution. |
|
| Substitute 4 for x:
Simplify. |
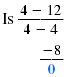 |
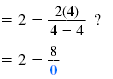 |
The result is division by zero, which is undefined.
This means that x = 4 is not a solution.
Therefore, the equation has no solution.
We call 4 an extraneous solution. It is a number that results from
solving an equation, but it is not a solution of the equation.
Since it does not satisfy the original equation, an extraneous solution
is not really a solution. An extraneous solution is sometimes called a
false solution.
Example
Solve:
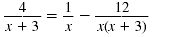
Solution
Multiply each side by x(x + 3), the LCD of the rational expression.
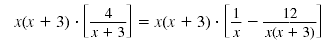
Distribute x(x + 3) to each term on the right side.
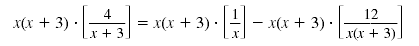
| Cancel common factors.
|
4x |
= x + 3 - 12 |
| Subtract x from both sides
and simplify the right side. |
3x |
= -9 |
| Divide both sides by 3. |
x |
= -3 |
| It appears that x = -3 is a solution.
|
|
|
| However, if we substitute -3 for x in the original equation
the result is division by 0. |
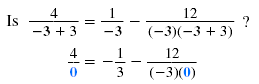 |
Division by 0 is undefined, so x = -3 is not a solution.
Therefore, the equation has no solution.
|