Polynomials
Adding and Subtracting Polynomials
EXAMPLE
Add or subtract the following polynomials.
(a) (8x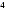 - 4x - 4x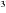 + 6x) +
(3x + 6x) +
(3x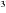 + 5x
+ 5x - 9x + 8)
- 9x + 8)
Solution
Combine like terms.
(8x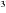 - 4x - 4x + 6x) + (3x + 6x) + (3x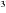 + 5x + 5x - 9x + 8) - 9x + 8)
= (8x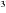 + 3x + 3x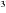 ) + (- 4x ) + (- 4x + 5x + 5x ) + (6x -
9x) + 8 ) + (6x -
9x) + 8
= 11x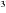 + x + x -3x + 8 -3x + 8
(b) (-4x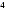 + 6x + 6x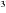 - 9x - 9x - 12) +
(-3x - 12) +
(-3x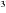 + 8x
+ 8x - 11x + 7)
- 11x + 7)
Solution
Combining like terms as before yields .
-4x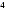 + 3x + 3x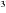 - x - x - 11x - 5 - 11x - 5
(c) (2x - 11x + 8) - (7x - 11x + 8) - (7x - 6x + 2) - 6x + 2)
Solution
Distributing the minus sign yields
(2x - 11x + 8) + (-7x
- 11x + 8) + (-7x + 6x - 2) + 6x - 2)
= -5x - 5x + 6 - 5x + 6
Multiplying Polynomials
The distributive property is also used to multiply
polynomials, along with the fact that 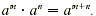 For
example, For
example,

EXAMPLE
Multiply.
(a) 8x(6x - 4)
Solution
8x(6x - 4) = 8x(6x) - 8x(4)
= 48x - 32x - 32x
(b) (3p - 2)(p + 5p - 1) + 5p - 1)
Solution
(3p - 2)(p + 5p - 1) + 5p - 1)
= 3p(p + 5p - 1) -2(p + 5p - 1) -2(p + 5p - 1) + 5p - 1)
= 3p(p ) + 3p(5p) + 3p(-1) -2(p ) + 3p(5p) + 3p(-1) -2(p ) -2(5p)
-2(-1) ) -2(5p)
-2(-1)
= 3p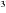 + 15p + 15p -3p -2p -3p -2p - 10p + 2 - 10p + 2
= 3p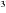 + 13p + 13p -13p + 2 -13p + 2
(c) (x + 2)(x + 3)(x - 4)
Solution
(x + 2)(x + 3)(x - 4)
= [(x + 2)(x + 3)](x - 4)
= (x + 2x + 3x + 6)(x - 4) + 2x + 3x + 6)(x - 4)
= (x + 5x + 6)(x - 4) + 5x + 6)(x - 4)
= x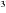 + 5x + 5x + 6x -4x + 6x -4x - 20x - 24 - 20x - 24
= x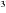 + x + x - 14x - 24 - 14x - 24
|