Multiply by the Reciprocal
Two numbers are reciprocals if their product is 1. Since 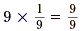 , this means that 9 and , this means that 9 and 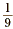 are reciprocals. are reciprocals.
• The numbers 4 and 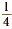 are reciprocals, since are reciprocals, since 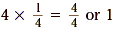 . .
• The fractions 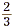 and and 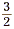 are reciprocals, since are reciprocals, since 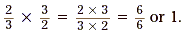
Key Idea
The reciprocal of any fraction can be obtained by inverting
the fraction. In other words, the denominator of the original
fraction becomes the numerator and the numerator of the original
fraction becomes the denominator. In symbols, the reciprocal of
is 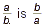 . .
• 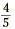 is the reciprocal of is the reciprocal of 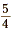 . .
• 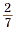 is the reciprocal of is the reciprocal of 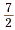 . .
• 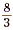 is the reciprocal of is the reciprocal of 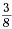 . .
Since 7 ÷ 9 and 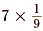 are both equal to are both equal to 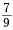 , then , then 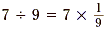 . Also, we know that 9 and . Also, we know that 9 and 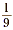 are reciprocals. So, dividing by a number
and multiplying by the reciprocal of that number give the same
result. are reciprocals. So, dividing by a number
and multiplying by the reciprocal of that number give the same
result.
We can easily find that 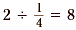 . Since 2 × 4 is also 8, this means that . Since 2 × 4 is also 8, this means that 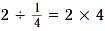 . So, dividing by a fraction and
multiplying by its reciprocal give the same result. . So, dividing by a fraction and
multiplying by its reciprocal give the same result.
Key Idea
Dividing a number by a fraction is equivalent to multiplying
the number by the reciprocal of the fraction.
|