Comparing Fractions
Some situations require us to compare fractions, that is, to
rank them in order of size.
For instance, suppose that 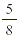 of one airline’s flights arrive on time, in contrast to of
of one airline’s flights arrive on time, in contrast to of 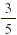 another airline’s flights. To decide which airline has a
better record for on-time arrivals, we need to compare the
fractions.
another airline’s flights. To decide which airline has a
better record for on-time arrivals, we need to compare the
fractions.
Or to take another example, suppose that the drinking water in
your home, according to a lab report, has 2 parts per million
(ppm) of lead. Is the water safe to drink? If the federal limit
on lead in drinking water is 15 parts per billion (ppb), again
you need to compare fractions.
One way to handle such problems is to draw diagrams
corresponding to the fractions in question. The larger fraction
corresponds to the larger shaded region.
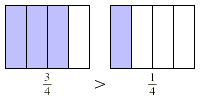
For instance, the diagrams show that 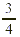 is greater than
is greater than 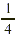 . The symbol > stands for “greater
than.” . The symbol > stands for “greater
than.”
Both 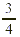 and and 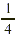 have the same denominator, so we can rank
them simply by comparing their numerators. have the same denominator, so we can rank
them simply by comparing their numerators.
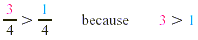
Note that the symbols < and > always point to the
smaller number.
For like fractions, the fraction with the
larger numerator is the larger fraction.
Definitions
Like fractions are fractions with the same
denominator.
Unlike fractions are fractions with different
denominators.
To Compare Fractions
- compare the numerators of like fractions, and
- express unlike fractions as equivalent fractions having
the same denominator and then compare their numerators.
EXAMPLE 1
Compare 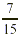 and and 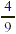 . .
Solution
These fractions are unlike because they have different
denominators. Therefore we need to express them as equivalent
fractions having the same denominator. But what should that
denominator be?
One common denominator that we can use is the product of the
denominators: 15 · 9 = 135
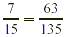 , 135 = 15 · 9 so the new numerator is 7 · 9, or
63. , 135 = 15 · 9 so the new numerator is 7 · 9, or
63.
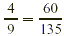 , 135 = 9 · 15, so the new numerator is 4 · 15, or
60. , 135 = 9 · 15, so the new numerator is 4 · 15, or
60.
Next, we compare the numerators of the like fractions that we
just found.
Because 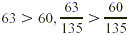 . Therefore . Therefore 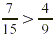 . .
Another common denominator that we can use is the least common
multiple of the denominators.

The LCM is 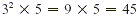 . We then compute the equivalent
fractions. . We then compute the equivalent
fractions.
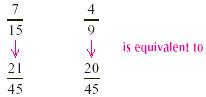
Because 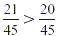 , we know that , we know that 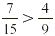 . .
Note that in Example 1 we computed the LCM of the two
denominators. This type of computation is used frequently in
working with fractions.
Definition
For any set of fractions, their least common
denominator (LCD) is the least common multiple of their
denominators.
In Example 2, pay particular attention to how we use the LCD.
EXAMPLE 2
Order from smallest to largest: 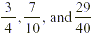 . .
Solution
Because these fractions are unlike, we need to find equivalent
fractions with a common denominator. Let’s use their LCD as
that denominator.
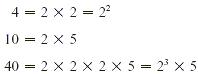
The LCD 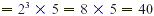 . Check: 4 and 10 are both factors of 40. . Check: 4 and 10 are both factors of 40.
We write each fraction with a denominator of 40.
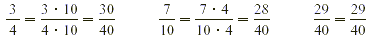
Then we order the fractions from smallest to largest. (The
symbol < stands for “less than.”)
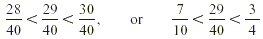
EXAMPLE 3
About 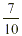 of Earth’s surface is covered by
water and of Earth’s surface is covered by
water and 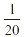 is covered by desert. Does water or
desert cover more of Earth? is covered by desert. Does water or
desert cover more of Earth?
Solution
We need to compare 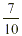 with
with 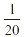 . .
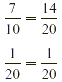
Since 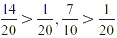 . Therefore water covers more of Earth
than desert does. . Therefore water covers more of Earth
than desert does.
|