Product and Quotient of Functions
We will evaluate the product and quotient of two functions for a
given number. We will use the same two methods as we did for the sum
and difference of two functions.
For the first example, we will use one specific method. In fact, we will first multiply
the functions and then we will evaluate the product for a specific value of x.
Example 1
Given f(x) = x2 + 6 and g(x) = x2 - 5, find (f
· g)(x) when x = 3. That is, find (f
· g)(3).
Solution
| Step 1 |
Find (f · g)(x).
Substitute for f(x) and g(x).
Multiply (use FOIL).
Combine like terms.
Thus, (f · g)(x) = x4 + x2 - 30 |
(f
· g)(x) |
= f(x) · g(x)
= (x2 + 6) · (x2
- 5)
= x4 - 5x2 + 6x2
- 30
= x4 + x2 - 30 |
| Step 2 |
Use x = 3 to find (f · g)(3). Substitute 3 for x.
Simplify. |
|
= (3)4 +
(3)2 - 30
= 60 |
So, (f · g)(3) = 60
Example 2
Given f(x) = 12x3 - 18x and g(x) = 3x, find
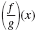 when x
= -8.
That is, find
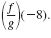
Solution
Note:
One way to simplify
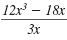 is to factor and then cancel common
factors:
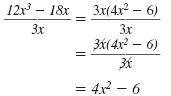
A second way to simplify
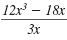
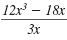
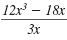is to write it as two
fractions and then simplify each.
|
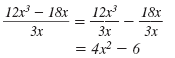
