Operations with Monomials

A monomial is an algebraic expression that is a constant or a product of a constant and one or more variables with whole number exponents.

Monomials:

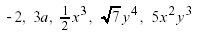
Basic Rules for Exponents

1. Extending the Multiplying of “powers with the same base”: a ^m · a ⁿ · a ^p =a ^{m + n + p}

Add exponents by the rules of adding signed numbers where m, n, p { integers}

Example 1:

a) z ⁵ · z ² · z ⁴ = z ⁵⁺²⁺⁴ = z ¹¹

b) x ² · x ³ · x ⁴ · x ⁵ = x ^2+3+4+5 = x ¹⁴

2. Powering of powers:

For base a and exponents m, n { natural numbers }

(a ^m) ⁿ = a ^m·n

Example 2:

a) (x ⁴ )³ = x ^4·3 = x ¹²

b) (y ²) ⁵ = y^2·5 = y ¹⁰

3. Powering of products with different bases a and b, and exponent n { natural numbers}

(a·b) ⁿ = a ⁿ · b ⁿ

NOTE: The exponent affects only the number that it immediately touches so you must always put negative numbers in parentheses ( ).

Example 3:

1. (x ⁵ y ⁷)³ = (x ⁵)³Â·(y ⁷)³ = x^5·3·y^7·3 = x¹⁵ y²¹ Apply properties and multiply exponents.

2. (-2 · x²y³)⁴ = (-2)⁴ ·(x²)⁴·(y³)⁴ = 16 ·(x^2·4)·(y^3·4) = 16 · x⁸y¹² Apply properties, multiply exponents.

Definition of Negative Exponent 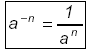Note: a ^-n × a ⁿ = 1 They are reciprocals.

The sign in the exponent does not affect the sign of the number in the base.

Example 4:

a) 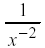Since -2 is in the denominator place positive in the numerator:

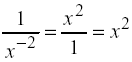
b) x ^-8  Since -8 is in the numerator place positive in the denominator:

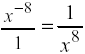
Definition of Zero Exponent a ⁰ = 1 Note: The result of raising any base to the 0 exponent will always be 1. (a ≠ 0)

1. (57x⁹ y³² z ⁻²⁵ )⁰ = 1

4. Division of powers with positive exponents:

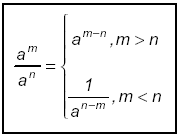Subtract the smaller exponent from the larger exponent and put the resulting “power ” in the “place” of the larger “power”. Put a 1 in the numerator if the larger “power” is in the denominator.

Example 5: (Working with positive exponents):

1. 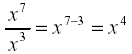[7 > 3 result goes in the numerator.]

2. 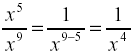[9 > 5 result goes in the denominator.]

3. 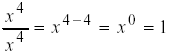[4 = 4 Exponents the same result is always 1.]