Using the Discriminant in Factoring

Consider ax² + bx + c, where a, b, and c are integers with a greatest common factor of 1. If b² - 4ac is a perfect square, then is a whole number, and the solutions to ax² + bx + c = 0 are rational numbers. If the solutions to a quadratic equation are rational numbers, then they could be found by the factoring method. So if b² - 4ac is a perfect square, then ax² + bx + c factors. It is also true that if b² - 4ac is not a perfect square, then ax² + bx + c is prime.

Example 1

Using the discriminant

Use the discriminant to determine whether each polynomial can be factored.

a) 6x² + x - 15

b) 5x² - 3x + 2

Solution

a) Use a = 6, b = 1, and c = -15 to find b² - 4ac:

b² - 4ac = 1² - 4(6)(-15) = 361

Because 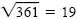, 6x² + x - 15 can be factored. Using the ac method, we get

6x² + x - 15 = (2x - 3)(3x + 5).

b) Use a = 5, b = -3, and c = 2 to find b² - 4ac:

b² - 4ac = (-3)² - 4(5)(2) = -31

Because the discriminant is not a perfect square, 5x² - 3x + 2 is prime.