Factoring Polynomials
Before factoring any polynomial, write the polynomial in
descending order of one of the variables. Then note how many
terms there are, and proceed by using one or more of the
following techniques.
1. If there are THREE TERMS
, look for these patterns:
a. Quadratic trinomials of the form ax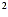 + bx + c where a = 1 (QT a = 1) factor into the product of two
binomials (double bubble) where the factors of c must add to b.
+ bx + c where a = 1 (QT a = 1) factor into the product of two
binomials (double bubble) where the factors of c must add to b.
Example: x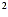 - 4x - 12 = (x - 6)(x + 2) - 4x - 12 = (x - 6)(x + 2)
b. Quadratic trinomials of the form ax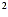 + bx + c where a
+ bx + c where a 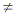 1 (QT a 1 (QT a 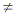 1) eventually factor into the product of two binomials (double
bubble) but you must first find the factors of ac that add to b,
rewrite the original replacing b with these factors of ac, then
factor by grouping to finally get to the double bubble.
1) eventually factor into the product of two binomials (double
bubble) but you must first find the factors of ac that add to b,
rewrite the original replacing b with these factors of ac, then
factor by grouping to finally get to the double bubble.
Example: 9x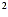 + 15x + 4 + 15x + 4
ac = (9)(4) = 36
factors of 36 that add to 15: 12 and 3
9x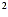 + 12x + 3x + 4 rewrite 15x as 12x + 3x, then factor
by grouping 3x(x + 4) + 1(x + 4) = (x + 4)(3x + 1) + 12x + 3x + 4 rewrite 15x as 12x + 3x, then factor
by grouping 3x(x + 4) + 1(x + 4) = (x + 4)(3x + 1)
c. Quadratic square trinomials (QST) of the
form ax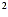 + bx + c may factor into the square of a binomial.
Look for the pattern where two of the terms are perfect squares,
and the remaining term is twice the product of the square root of
the squares: + bx + c may factor into the square of a binomial.
Look for the pattern where two of the terms are perfect squares,
and the remaining term is twice the product of the square root of
the squares:
a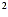 ± 2ab + b ± 2ab + b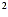 = (a ± b)
= (a ± b)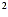
Example: 16x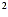 - 40x + 25 = (4x - 5) - 40x + 25 = (4x - 5)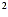
Note the pattern: Square root of 16 x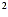 is 4 x. Square root of 25 is 5.
is 4 x. Square root of 25 is 5.
Twice the product of the square roots: 2(4x)(5) = 40x, which
is the middle term
2. Factor all expressions completely.
Sometimes, you will need to use two or three types of factoring
in a single problem.
Example: -2x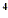 + 32 + 32
-2x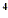 + 32 = factor out the GCF of -2x + 32 = factor out the GCF of -2x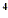 and 32
and 32
-2(x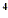 - 16) = factor the difference of squares - 16) = factor the difference of squares
-2(x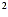 - 4)(x - 4)(x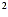 + 4) = factor the remaining difference of squares
+ 4) = factor the remaining difference of squares
-2(x - 2)(x + 2)(x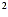 + 4) (remember that the sum of squares is prime)
+ 4) (remember that the sum of squares is prime)
|