Solving Compound Linear Inequalities

A compound inequality contains two inequality symbols.

For example, to indicate all the numbers between -4 and 6 we could write the following: -4 < x and x < 6

This says that -4 is less than x and x is also less than 6.

We can say the same thing using this compound inequality: -4 < x < 6

To solve a compound inequality, apply the same operations to the left side, the middle part, and the right side. A compound inequality is solved when the variable has been isolated in the middle part.

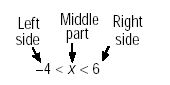
Example 1

Solve: 25 ≥ 1 - 4y > 1. Then, graph the solution on a number line.

Solution	25 ≥	1 - 4y	> 1
Subtract 1 from each part. Simplify.	25 - 1 ≥ 24 ≥	1 - 4y - 1 -4y	> 1 - 1 > 0
Divide each part by -4. Since we are dividing by a negative, we must reverse both of the inequality symbols.	≤
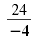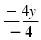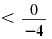Simplify.	-6 ≤	y	< 0

The compound inequality -6 ≤ y < 0 includes all real numbers between -6 and 0, including -6.

To graph the solution, plot a closed circle at -6 and an open circle at 0. Then, shade the region between -6 and 0.

Example 2

Solve: 3 + x < 4x - 6 < 9 + x. Then, graph the solution on a number line.

Solution Subtract x from each part. Simplify. Add 6 to each part. Simplify.	3 + x < 3 + x - x < 3 < 3 + 6 < 9 <	4x - 6 4x - 6 - x 3x - 6 3x - 6 + 6 3x	< 9 + x < 9 + x - x < 9 < 9 + 6 < 15
Divide each part by 3.
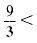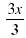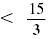Simplify.	3 <	x	< 5

To graph the solution, place an open circle at 3 and an open circle at 5. Then, shade the region between the plotted points.
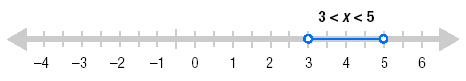