Solving Rational Equations
After studying this lesson, you will be able to:
- Solve rational equations.
To solve an equation with fractions (rational equations),
multiply each term by a common denominator. This will eliminate
the fractions. Then, solve the equation that remains.
Example 1
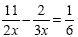
The common denominator is 6x so we multiply each term by 6x:
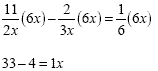 |
Now, we have 3 multiplications to do -
this will eliminate the variables |
| Collect like terms |
| 29 = x |
|
**remember, the solution cannot cause any denominator to equal
zero - if it does, it is an extraneous solution
Example 2

The common denominator is 60 so we multiply each term by 60:
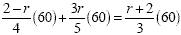 |
Now, we have 3 multiplications to do -
this will eliminate the variables |
| 30 - 15r + 36r = 20r + 40 |
Collect like terms |
| 30 + 21r = 20r + 40 |
Get the variables together by subtracting
20r from each side |
| 30 + r = 40 |
Subtract 30 from each side |
| r = 10 |
|
Example 3
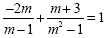
To find the common denominator we have to factor the second
denominator:
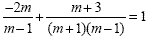
The common denominator is (m + 1) (m - 1) so we multiply each
term by (m + 1) (m - 1):
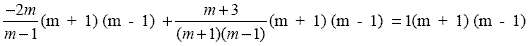
Now, we have 3 multiplications to do - cancel out identical
binomials
| -2m ( m + 1 ) + (m + 3 ) = m 2
- 1 |
Multiply |
| -2m 2 - 2m + m + 3 = m 2
- 1 |
Collect like terms. |
| -2m 2 - m + 3 = m 2
- 1 |
This is a quadratic equation so we need
to set it equal to zero. Let's move all terms to the
right side. |
| 0 = 3m 2 + m - 4 |
|
Now, factor and set each factor equal to zero and solve.
0 = (3m + 4) ( m - 1 )
| 3m + 4 = 0 |
m - 1 = 0 |
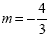 |
m = 1 |
m = 1 is an extraneous solution because it will cause a
denominator to equal zero.
|