Evaluating Trigonometric Functions
There are two ways to evaluate trigonometric functions: (1) decimal approximations
with a calculator (or a table of trigonometric values) and (2) exact evaluations using
trigonometric identities and formulas from geometry. When using a calculator to
evaluate a trigonometric function, remember to set the calculator to the appropriate
mode—degree mode or radian mode.
Example 1
Exact Evaluation of Trigonometric Functions
Evaluate the sine, cosine, and tangent of
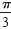 . .
Solution
Begin by drawing the angle θ = π/3 in standard position, as shown in
the figure below.
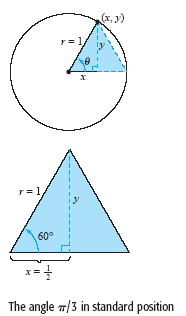
Then, because 60º = π/3 radians, you can draw an equilateral triangle
with sides of length 1 and θ as one of its angles. Because the altitude of this triangle
bisects its base, you know that
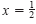 . Using the Pythagorean Theorem, you obtain . Using the Pythagorean Theorem, you obtain
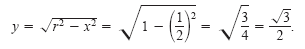
Now, knowing the values of x, y, and r, you can write the following.
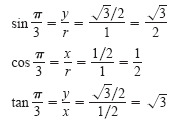
NOTE All angles in this text are measured in radians unless stated otherwise. For example,
when we write sin 3, we mean the sine of 3 radians, and when we write sin 3º, we mean the sine
of 3 degrees.
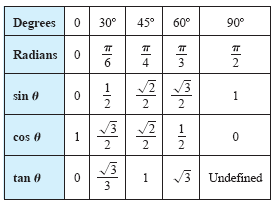
The degree and radian measures of several common angles are given in the table
below, along with the corresponding values of the sine, cosine, and tangent (see
the figure below).
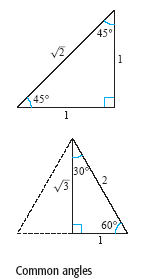
Common First Quadrant Angles
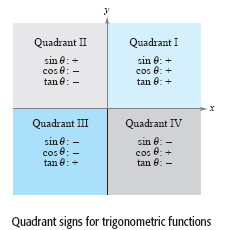
The quadrant signs for the sine, cosine, and tangent functions are shown in
the figure below.
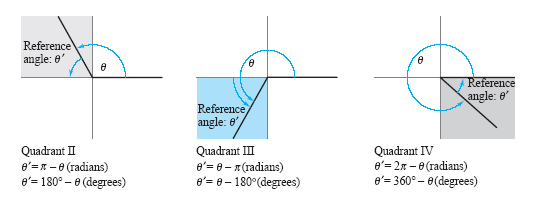
To extend the use of the table on the preceding page to angles in quadrants other
than the first quadrant, you can use the concept of a reference angle (see
the figure below), with the appropriate quadrant sign. For instance, the reference angle for
3π/4 is π/4and because the sine is positive in the second quadrant, you can write
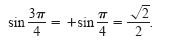
Similarly, because the reference angle for 330º is 30º, and the tangent is negative in
the fourth quadrant, you can write

Example 2
Trigonometric Identities and Calculators
Evaluate the trigonometric expression.
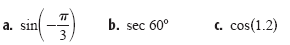
Solution
a. Using the reduction formula sin(-θ) =
-sin θ, you can write
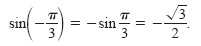
b. Using the reciprocal identity sec θ = 1/ cos
θ, you can write
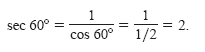
c. Using a calculator, you can obtain cos(1.2) ≈
0.3624.
Remember that 1.2 is given in radian measure. Consequently, your calculator must
be set in radian mode.
|