Solving Equations by Multiplying or Dividing
Objective Learn to solve multiplication and
division equations.
This lesson uses one of the most important ideas in algebra,
the Multiplication Property of Equality. Make sure you understand
how it is being used.
Solving Equations by Multiplying or Dividing
Luisa is three times as old as Justin. If Luisa is 24 years
old, how old is Justin?
In this problem, two quantities are equal to each other. In
words, three times Justin's age is equal to Luisa's age. Luisa's
age is 24, but we don't know Justin's age. When we do not know a
quantity, we choose a letter as a placeholder for that value so
we can work with the other numbers in the problem and perhaps
determine the unknown quantity. The letter is called a variable.
In this case, let's write j for Justin's age. The quantity
"three times Justin's age" is now represented by 3j.
Since three times Justin's age is equal to Luisa's age, we now
write
3j = 24.
This expression is called an equation. If an
equality results when a number is substituted for j, the number
is a solution to the equation.
In order to determine j, we'll need to use an important
property of equations.
Key Idea
Multiplying or dividing any equation by a nonzero number
results in a true equation. Any solution of the original equation
will be a solution of the new equation, and any solution of the
new equation will be a solution of the original equation.
These ideas are called the Multiplication and Division
Properties of Equality. In 3j = 24, we want to isolate the
variable j on the left side, so that the equation reads
j = ?
where the ? is a quantity we have to determine that doesn't
involve the variable j. Once the equation is in this form, it is
solved since weknow that j is equal to the number on the right
side.
Let' s solve the equation to dete rmine Justin's age.
| 3j = 24 |
|
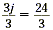 |
Divide each side by 3 |
| j = 8 |
Simplify. |
So Justin is 8 years old. Let's solve another equation using
the Division Property of Equality.
Example 1
Solve 7x = 112.
Solution
| 7x = 112 |
|
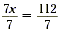 |
Divide each side by 7 |
| x = 16 |
Simplify. |
The solution is 16.
The next example shows how to solve an equation using the
Multiplication Property of Equality.
Example 2
Solve 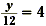 . .
Solution
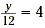 |
|
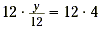 |
Multiply each side by 12 |
| x = 16 |
Simplify. |
The solution is 48.
How does this work? To answer this question, think of the
general pattern. For an equation of the form
(coefficient) · x = number, we divide the whole equation by
the coefficient to get
 . .
|