Multiplying and Dividing With Square Roots
The following rules for multiplication and division with
algebraic square roots are the same as those for numerical square
roots:
- Property 1:
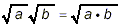
- Property 2:
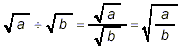
where ‘a’ and ‘b’ stand for any valid
mathematical expression.
Example 1:
Simplify 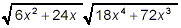
solution:
We can simply go ahead and apply property (1), getting
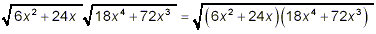
But now, we need to recall that simplification of square roots
involves finding perfect square factors in the square root, so
there is no point in expanding the product of the two binomials
in this square root. Instead, we check for the possibility of
further factoring
6x 2 + 24x = 6x(x + 4)
and
18x 4 + 72x 3 = 18x 3(x + 4)
Thus
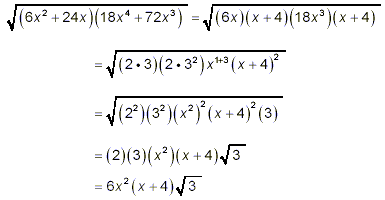
Example 2:
Expand and simplify 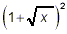
solution:
At the start, this example involves the square of a binomial.
You can use either of the two approaches presented earlier for
multiplying one binomial by another binomial. The result here is
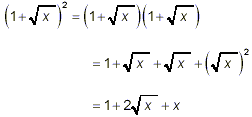
as the final answer.
Two errors are commonly made with this type of problem:
(1) People sometimes just square each term of the binomial:
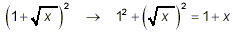
But, you know that this is not the correct way to expand what
amounts to the product of two binomials.
(2) People sometimes forget the obvious simplification that 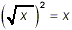 , leaving their answer
as , leaving their answer
as
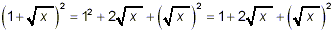
instead of
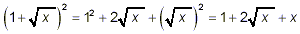
Example 3:
Expand and simplify 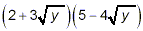
solution:
This example is very similar to the problem in Example 2 above
– the product of two binomials, each of which contains a
square root. We get
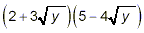
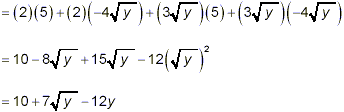
as the final result.
Example 4:
Expand and simplify 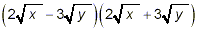
solution:
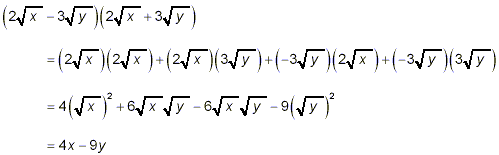
as the final result. The two middle terms in the second last
line are identical but of opposite sign, and so cancel each
other. This sort of pattern of binomial factors, where each
binomial contains square roots but their product contains no
square roots, is the basis for methods to rationalize
denominators of fractions which have binomial denominators.
Example 5:
Simplify 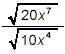
solution:
We can use either of two approaches here. We could start by
using property (2) from the beginning of this document to write
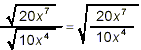
and then simplify the fraction in the square root to get
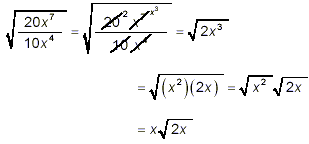
as a final, simplified answer. This approach is quite short
and efficient.
A second approach is to simplify the square roots first
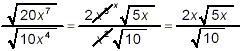
and then rationalize the denominator:
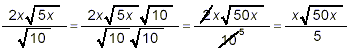
But
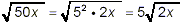
and so
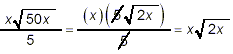
which is exactly the same final answer as we obtained with the
first method.
|