Quadratic Inequalities
A quadratic inequality has the form ax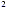 + bx + c > 0 (or <, or
+ bx + c > 0 (or <, or 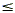 , or , or 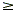 ). The highest exponent is 2. The next few
examples show how to solve quadratic inequalities. ). The highest exponent is 2. The next few
examples show how to solve quadratic inequalities.
Solving Quadratic Inequalities
EXAMPLE
Solve the quadratic inequality x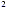 - x < 12.
- x < 12.
Solution
Write the inequality with 0 on one side, as x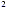 - x - 12 < 0. This inequality is solved with values of x that
make x
- x - 12 < 0. This inequality is solved with values of x that
make x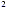 - x - 12 negative (< 0). The quantity x - x - 12 negative (< 0). The quantity x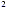 - x - 12 changes from positive to negative or from negative to
positive at the points where it equals 0. For this reason, first
solve the equation x
- x - 12 changes from positive to negative or from negative to
positive at the points where it equals 0. For this reason, first
solve the equation x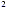 - x - 12 = 0.
- x - 12 = 0.
x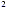 - x - 12 = 0 - x - 12 = 0
(x - 4)(x + 3) = 0
x = 4 or x = -3
Locating -3 and 4 on a number line, as shown in Figure 3,
determines three intervals A, B, and C.
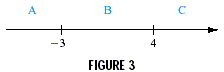
Decide which intervals include numbers that make x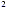 - x - 12 negative by substituting any number from each interval
in the polynomial. For example,
- x - 12 negative by substituting any number from each interval
in the polynomial. For example,
choose -4 from interval A: (-4)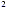 - (-4) - 12 = 8 > 0;
- (-4) - 12 = 8 > 0;
choose 0 from interval B: 0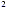 - 0 - 12 = -12 < 0;
- 0 - 12 = -12 < 0;
choose 5 from interval C: 5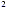 - 5 - 12 = 8 > 0.
- 5 - 12 = 8 > 0.
Only numbers in interval B satisfy the given inequality, so
the solution is (-3, 4). A graph of this solution is shown in
Figure 4.
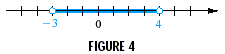
Solving Polynomial Inequalities
EXAMPLE
Solve the inequality x(x-1)(x+3) 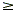 0. 0.
Solution
This is not a quadratic inequality. If the three factors are
multiplied, the highest-degree term is x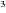 . However, it can be solved in the same way as a
quadratic inequality because it is in factored form. First solve
the corresponding equation. . However, it can be solved in the same way as a
quadratic inequality because it is in factored form. First solve
the corresponding equation.
x(x - 1)(x + 3) = 0
x = 0 or x - 1 = 0 or x + 3 = 0
x = 0 or x = 1 or x = -3
These three solutions determine four intervals on the number
line: 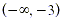 , (-3, 0), (0, 1) and , (-3, 0), (0, 1) and 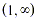 . Substitute a number from each interval into the
original inequality to determine that the solution includes the
numbers less than or equal to -3 and the numbers that are equal
to or between 0 and 1. See Figure 5. . Substitute a number from each interval into the
original inequality to determine that the solution includes the
numbers less than or equal to -3 and the numbers that are equal
to or between 0 and 1. See Figure 5.
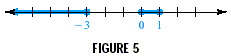
In interval notation, the solution is
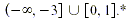
* The symbol 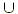 indicates the union of two sets, which
includes all elements in either set. indicates the union of two sets, which
includes all elements in either set.
|