Rational Expressions
Many algebraic fractions are rational expressions, which are
quotients of polynomialswith nonzero denominators. Examples
include
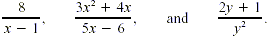
Properties for working with rational expressions are
summarized next.
PROPERTIES OF RATIONAL EXPRESSIONS
For all mathematical expressions P , Q , R , and S , with Q
and S 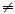 0. 0.
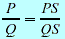 Fundamental property Fundamental property
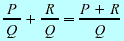 Addition Addition
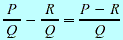 Subtraction Subtraction
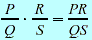 Multiplication Multiplication
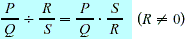 Division Division
When using the fundamental property to write a rational
expression inlowest terms, we may need to use the fact that 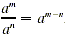
For example,
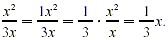
Reducing Rational Expressions
EXAMPLE
Write each rational expression in lowest terms, that is,
reduce the expression as much as possible.
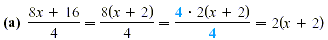
Factor both the numerator and denominator in order to identify
any commonfactors, which have a quotient of 1. The answer could
also be written as 2x + 4
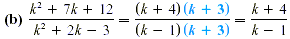
The answer cannot be further reduced.
CAUTION
One of the most common errors in algebra involves incorrect
useof the fundamental property of rational expressions. Only
common factors may be divided or “canceled.” It is
essential to factor rational expressions beforewriting them in
lowest terms. In Example 1(b), for instance, it is not correctto
“cancel” k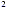 (or cancel k, or divide 12 by -3) because the additions and
subtraction must be performed first. Here they cannot be
performed, so it is notpossible to divide. After factoring,
however, the fundamental property can beused to write the
expression in lowest terms.
(or cancel k, or divide 12 by -3) because the additions and
subtraction must be performed first. Here they cannot be
performed, so it is notpossible to divide. After factoring,
however, the fundamental property can beused to write the
expression in lowest terms.
|