Factoring Polynomials
Example 1
Complete the diagram to find the GCF of polynomials A, B, and C.
Solution
| Factor each polynomial. |
12x2y 18xy3
10xy |
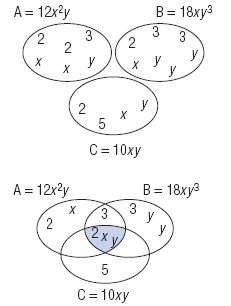
= 2 · 2 · 3 · x
· x · y = 2 · 3 · 3 · x · y · y · y
= 2 · 5 · x · y |
|
| For each polynomial, write the factors in the corresponding circle. Since 3 is a factor of A and B only, write 3 where the circles for A and B
overlap.
Since 2, x, and y are factors of A, B, and C, write 2, x, and y in the region
where all three circles overlap.
The common factors lie in the region where all three circles overlap.
The factors in that region are 2, x, and y.
Therefore, the GCF of the polynomials is 2
· x · y = 2xy. |
 |
Example 2
Complete the table.
Then, write the polynomial and its factorization.
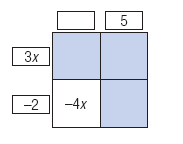
Solution
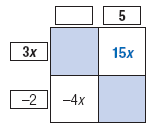
| Multiply 3x by 5 to get 15x.
Write this term in the upper right box. |
 |
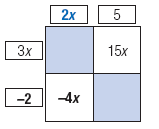 |
Ask yourself, "The term -4x is the product of -2 and what?"
The answer is 2x.
Therefore, write 2x above the upper left box. |
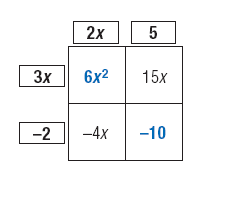 |
Multiply 3x by 2x to get 6x2. Write this term in the upper left box. Likewise, multiply
-2 by 5 to get -10. Write this term in the lower right
box.
The sum of the terms in the boxes is
6x2 + 15x - 4x - 10 = 6x2 + 11x - 10.
The terms outside of the large square represent the two binomials,
(2x + 5) and (3x - 2), that are the factors of the trinomial.
That is, 6x2 + 11x - 10 = (2x + 5)(3x - 2). |
|