Laws of Exponents
(i) multiplication of two powers:
if c is any number, then
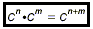
(ii) division of one power by another:
if c is any nonzero number, and m is a larger number than n,
then
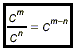
if c is any nonzero number, and m is a larger number than n,
then
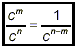
(iii) raising a power to a power:
if c is any number, then
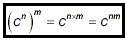
(iv) raising a product to a power:
if c and d are any numbers,
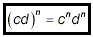
(v) raising a quotient or a fraction to a power:
if c is any number, and d is any nonzero number, then
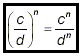
(vi) A Caution!
The five “laws” of exponents summarized in the
square boxes above all involve multiplication or division only.
As soon as addition or subtraction occurs, the obvious relations
are NOT TRUE!
For example,
( 2 + 3 ) 4 = 5 4 = 625
but
( 2 + 3 ) 4 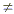 2 4
+ 3 4, 2 4
+ 3 4,
since this latter expression evaluates to 16 + 81 = 97, which
is clearly incorrect. Another example is
( 7 - 4 ) 5 = 3 5 = 243
but
( 7 - 4 ) 5 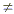 7 5
- 4 5, 7 5
- 4 5,
since the latter gives 16807 – 1024 = 15783, which is
clearly wrong. In both of these cases, the rules of priority for
operations (described just ahead in these topic notes) are
followed in the correct forms. It is necessary to evaluate the
quantity in brackets first, and then apply the exponent to the
result. The exponents here apply to the result of doing whatever
operations are shown inside the brackets. This will become a very
important rule to remember when the brackets contain symbolic
expressions rather than simple numerical expressions.
So, for powers of sums and differences, there is no simple law
(such as forms (iv) and (v) above for powers of products and
quotients, respectively) that allows us to express them in terms
of powers of the original terms in the sums or differences
themselves:
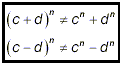
All of the properties of powers described in this section will
become even more useful when we deal with expressions involving
symbols rather than just numbers.
|