Solving Compound Inequalities
Objective Learn how to solve compound
inequalities.
In this lesson, we are dealing with compound
inequalities, expressions in which more than one inequality
applies to the same variable. When inequalities are multiplied by
a negative number, the inequality symbol must be reversed.
Compound Inequalities
Let's talk a little about the notation and the terminology.
A compound inequality is an expression like 3
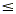 3x + 4 < 9 or 1x 3x + 4 < 9 or 1x 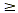 2 2 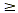 7. The two inequality symbols indicate that the
variable is to satisfy each part. So, for example, the inequality
2 < 2x - 5 < 4 is read “two is less than 2x - 5 and 2x
- 5 is less than four” or “2x - 5 is between 2 and
4”. 7. The two inequality symbols indicate that the
variable is to satisfy each part. So, for example, the inequality
2 < 2x - 5 < 4 is read “two is less than 2x - 5 and 2x
- 5 is less than four” or “2x - 5 is between 2 and
4”.
Solving Compound Inequalities
First, remember that solving an inequality (compound or
otherwise) means describing its solution set, since there is more
than one solution. Compound inequalities can be solved using the
same methods that are used to solve single inequalities, the
Addition and Multiplication Properties of Inequalities.
Example 1
Solve 3 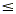 2 x + 1 2 x + 1 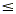 8. 8.
Solution
First, subtract 1 from each part so that no constants appear
in the expression that contains the variable.
3 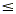 |
2x + 1 |
< 8 |
|
2 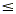 |
2x |
< 7 |
Subtract 1 from each part. |
1 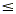 |
x |
< 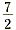 |
Divide each part by 2. |
The solution set is 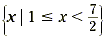
Why is this considered solving the inequality if, after all,
we still have an inequality? Why is this one any better than the
original inequality?
The answer is that the inequalities now apply directly to x,
not to an algebraic expression involving x. This means that it is
much easier to visualize the solution set, as the points to the
right of and including 1 and to the left of 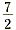 . Solving compound
inequalities means isolating x in the inequalities. . Solving compound
inequalities means isolating x in the inequalities.
Example 2
Solve -1 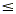 3 - x 3 - x 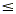 5. 5.
Solution
First, subtract 3 from each part to remove any constants from
the expression that contains x.
-1 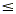 |
3 - x |
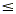 5 5 |
|
-4 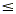 |
-x |
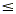 2 2 |
Subtract 3 from each side. |
Next, multiply each part of the inequality by -1 in order to
isolate x in the middle. Since -1 is negative, reverse the
inequality symbols.
4 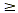 x x 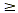 -2 -2
The solution set is { x | 4 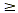 x x 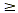 -2 }. -2 }.
|