Quadratic Functions: Parabolas
Quadratic Functions
A Quadratic (or Second-Degree) Function is a function of the form f(x)
= ax2 + bx + c, where a, b and c are real numbers and a
≠ 0. This form is called the General Form of a Quadratic
Function.
The graph of a quadratic function is a parabola with a "turning point" called the
vertex.
The domain of a quadratic function is all real numbers.
f(x) = x2 is concave up while f(x) = -x2 + 4x + 21 concave down.
So, when looking at the general form for a quadratic function, f(x) = ax2
+ bx + c, what does a tell us about the graph?
The sign of a tells us whether the parabola is concave up or concave down.
There is another form of a quadratic function, called the Standard Form of a Quadratic Function
y = a(x - h)2 + k is a quadratic function with vertex (h, k) and axis of symmetry x
= h. It opens up if a > 0 and down if a < 0. It is wider than f(x) = x2 if
-1 < a < 1, and narrower if a > 1 or if a < -1.
Now if the function is in General Form, f(x) = ax2 + bx + c, the vertex is not as obvious. There is a helpful formula, however:
Given a quadratic function f(x) = ax2 + bx + c, the vertex is the point:
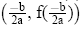
When you graph a Quadratic Function (parabola), you should show:
- Vertex
- Axis of Symmetry
- x-intercepts (or ) if it has any zeros
- y-intercept
|