Standard Form for the Equation of a Line
When we wrote the equation of a line in point-slope form, the equations
looked different depending on the point we chose. To show that the
equations are equivalent, rewrite each equation in standard form.
Definition —
Standard Form for the Equation of a Line
The standard form for the equation of a line is
Ax + By = C Where A, B, and C are real numbers and A and B are not both zero.
To write the equation of a line in standard form, move the terms with
variables to the left side and the constant term to the right side of the
equation.
Example 1
We can find the equation of the line that passes through
the points (-2, 7) and (6, 3).
We may use the point (6, 3) to obtain:
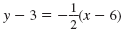
If we instead use (-2, 7), we obtain:
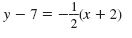
a. Write
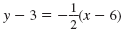 in standard form. in standard form.
b. Write
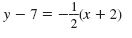 in standard form. in standard form.
c. What conclusion can you draw?
Solution
In each case, we want the x-term and y-term on the left side of the
equation. We want the constant term on the right side of the equation.
| a. |
To clear the fraction, multiply both
sides by 2.
|
2 · (y
- 3) |
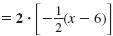 |
| |
Simplify.
Distribute -1.
Add x to both sides.
Add 6 to both sides.
|
2y - 6
2y - 6
x + 2y - 6
x + 2y |
= -1(x - 6)
= -x + 6
= 6
= 12 |
| b. |
To clear the fraction, multiply both
sides by 2. |
2 ·
(y - 7) |
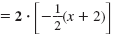 |
| |
Simplify.
Distribute -1.
Add x to both sides.
Add 14 to both sides. |
2y - 14
2y - 14
x + 2y - 14
x + 2y |
= -1(x + 2)
= -x - 2
= -2
= 12 |
c. In standard form, each equation is x + 2y = 12.
No matter which point we choose, we get the same result in standard form.
Note:
Ax + By = C
x + 2y = 12
Here, A is 1, B is 2, and C is 12.
|