Lines and Equations
⇒ We have built tables and plotted points for equations in the standard form:
Ax + By = C or the
slope-intercept form: y = m x + b and noted that (a , 0), or (x0 , 0), is the x-intercept and
(0, b), or (0, y0), is the y-intercept.
⇒ Now let us explore another equation given the slope-intercept form: y = m x + b:
where m is the slope and b (0 , b) is the y-intercept: y = mx + b.
Example.
Graph the linear equation 3x - 2y = 6 or
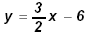
Compare this equation to the given the slope-intercept form: y = m x + b:
⇒ Write the slope
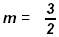 and the y-intercept b = - 6 or (0, b) = (0, - 6 ). and the y-intercept b = - 6 or (0, b) = (0, - 6 ).
Use the fact that the slope is
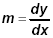 to find dx = 2 and dy = 3 to find dx = 2 and dy = 3
Now, build a table using the common differences. On the table put the point where x = 0 in the
middle of the x-sequence, add dx to get the next value below, and complete the x-sequence.
Look at the given table and see how it is started. Since both columns must be arithmetic sequences
use the value for dy and add it to b in the point (0, b) to complete the table and plot the points.
Build the table and plot the points: 3x - 2y = 6
| |
x |
y |
| |
-4 |
-9 |
|
dx = 2 |
-2 |
-6 |
dy = 3 |
| |
0 |
-3 |
| |
2 |
0 |
| |
4 |
3 |
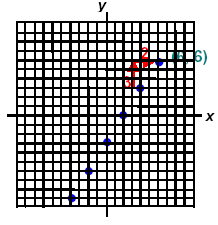
Check the a point (6, 6) not on your table by replacing x and y in the given equation.
3x - 2y = 6 → 3(6) - 2(6) = 6
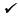
|