Interval Notation and Graphs
If an inequality involves a variable, then which real numbers can be used in
place of the variable to obtain a correct statement? The set of all such numbers
is the solution set to the inequality. For example, x < 3 is correct if x
is replaced by any number that lies to the left of 3 on the number line:
1.5 < 3, 0 < 3, and
-2 < 3
The set of real numbers to the left of 3 is written in set notation as {x
| x < 3}, in interval notation as (-∞,
3), and graphed below:
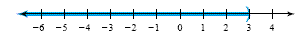
Note that -∞ (negative infinity) is not a number,
but it indicates that there is no end to the real numbers less than 3. The
parenthesis used next to the 3 in the interval notation and on the graph means
that 3 is not included in the solution set to x < 3.
An inequality such as x ≥ 1 is satisfied by 1
and any real number that lies to the right of 1 on the number line. The solution
set to x ≥ 1 is written in set notation as {x | x ≥ 1}, in interval notation as
[1, ∞), and graphed as below:
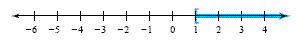
The bracket used next to the 1 in the interval notation and on the graph
means that 1 is in the solution set to x ≥ 1.
The solution set to an inequality can be stated
symbolically with set notation and interval notation, or visually with a graph.
Interval notation is popular because it is simpler to write than set notation.
The interval notation and graph for each of the four basic inequalities is
summarized as follows.
Basic Interval Notation (k any real number)
| Inequality |
Solution Set with Interval Notation |
Graph |
| x > k |
(k, ∞) |
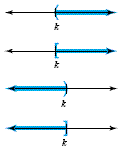 |
| x ≥ k |
[k, ∞) |
| x < k |
(-∞, k) |
| x ≤ k |
(-∞, k] |
Example
Interval notation and graphs
Write the solution set to each inequality in interval notation and graph it.
a) x > -5
b) x ≤ 2
Solution
a) The solution set to the inequality x > -5 is {x
| x > -5}. The solution set is the interval
of all numbers to the right of -5 on the number line. This set is written in
interval notation as (-5, ∞), and it is
graphed as follows:
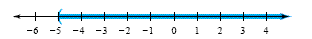
b) The solution set to x ≤ 2 is {x | x ≤ 2}.
This set includes 2 and all real numbers to the left of 2. Because 2 is included,
we use bracket at 2. The interval notation for this set is (-∞, 2]. The graph is
shown below.

|