Solving Equations with a Fractional Exponent
An expression that contains a fractional exponent can be written using a
radical. Fractional exponents are often referred to as rational exponents.
Definition — Rational Exponent
If a is a real number, and m and n are natural numbers, then:
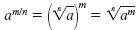
Here we assume that if n is even then a ≥
0.
Here are two examples:
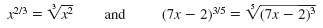
Notice that in am/n the number in the denominator of the fraction, n,
becomes the index in the radical,
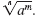
Example
Solve for x: (2x - 6)2/3 - 7 = -3
| Solution |
(2x - 6)2/3 - 7 |
= -3 |
| First, rewrite (2x - 6)2/3 as a radical. |
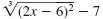 |
= -3 |
| Step 1 Isolate a radical term.
Add 7 to both sides.
Step 2 Apply the Principle of Powers. |
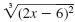 |
= 4 |
| Cube each side of the equation. |
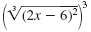 |
= (4)3 |
| Step 3 Solve the resulting equation.
Simplify.
Write the left side as a product.
Simplify.
|
(2x - 6)2
(2x - 6)(2x - 6)
4x2 - 24x + 36 |
= 64
= 64
= 64 |
| Write in standard form.
Divide both sides by 4.
Factor.
Use the Zero Product Property.
Solve for x.
Step 4 Check the solution.
|
4x2 - 24x - 28 x2 - 6x - 7
(x - 7)(x + 1)
x - 7 = 0 or x + 1
x = 7 or x |
= 0 = 0
= 0
= 0
= -1 |
We leave the check for you (both solutions check).
So, the solutions are x = 7 and x = -1.
|