Negative Rational Exponents
Negative integral exponents were defined by using reciprocals, and so are negative
rational exponents. For example, 8-2/3 is the reciprocal of 82/3.
So
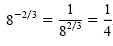
Negative Rational Exponents
If m and n are positive integers, then
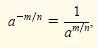 provided that a1/n is defined and nonzero. provided that a1/n is defined and nonzero.
Three operations are involved in evaluating the expression a-m/n. The operations
(root, power, reciprocal) can be performed in any order, but the simplest way
to evaluate a-m/n is usually the following order.
Evaluating -m/n

Example 2
Evaluating expressions with negative rational exponents
Evaluate each expression.
a) 4-3/2
b) (-27)-1/3
c) (-16)-3/4
Solution
a) The square root of 4 is 2. The cube of 2 is 8. The reciprocal of 8 is
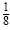 . So . So
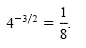
b) The cube root of -27 is -3. The first power of -3 is -3. The reciprocal of
-3 is
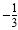 . So . So
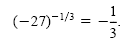
c) The expression (-16)-3/4 is not a real number because it involves the fourth
root (an even root) of a negative number.
|