Mixed Expressions and Complex Fractions
After studying this lesson, you will be able to:
- Simplify mixed expressions and complex fractions.
Example 1
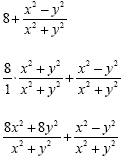 |
We need to convert the first fraction to
a common denominator |
| Multiply before adding |
| Add the numerators and keep the
denominator |
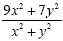 |
|
Example 2
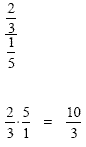 |
This is a complex fraction.
It can be read as "two-thirds divided by
one-fifth". Remember the rule for dividing
fractions is to multiply by the reciprocal:
|
Example 3
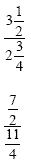 |
First we convert the mixed numbers to
improper fractions: Remember the rule for dividing
fractions is to multiply by the reciprocal:
|
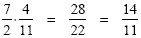 |
|
Example 4
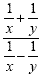
This is a complex fraction. The best way to approach this
problem is to work only with the numerator first. After we have
completely simplified the numerator, we will work on the
denominator. Then, the final step will be to divide the
fractions.
First, we're only going to work with the numerator:
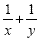 The common denominator
will be xy. We multiply the first fraction by The common denominator
will be xy. We multiply the first fraction by  and the second fraction by and the second fraction by 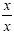 : :
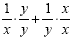 This will give us This will give us 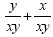 . Now we add to get . Now we add to get 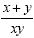
Now we go back and work with the denominator:
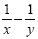 Add the opposite: Add the opposite: 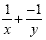
The common denominator will be xy. We multiply the first
fraction by 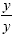 and the second fraction by and the second fraction by 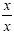 : :
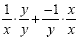 This will give us This will give us 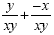 Now we add to get Now we add to get 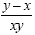
We have now simplified the numerator and the denominator to
get:
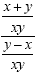
Now we have one fraction being divided by another. The rule
for dividing fractions is to multiply by the reciprocal.
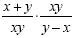 Now we multiply. (the xy and the xy will
cancel) Now we multiply. (the xy and the xy will
cancel) 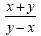
|