Intercepts Given Ordered Pairs and Lines
When a line crosses one, or both, of the axes the
point of the intersection is labeled “interceptâ€.
All points on the y-axis have the first element of zero.
The second element is a value of y where the line y = b intersects the line
x = 0. The point is labeled as (0, b)
and is called the y-intercept point.
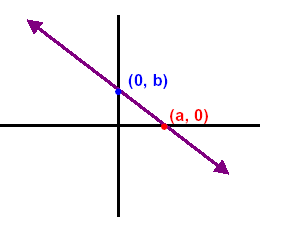
All points on the x-axis have the second element of zero.
The first element is a value of x where the line x = a
intersects the line y = 0. The point is labeled as (a, 0) and is called the
x-intercept point.
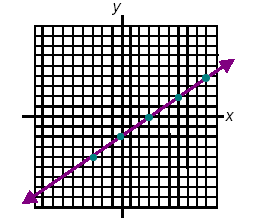
1. For the equation 2x − 3y = 6 complete the two points below.
2x − 3(0) = 6, x = 3 2(0) − 3y = 6, y = - 2
( 3 , 0 ) and ( 0 , -2 )
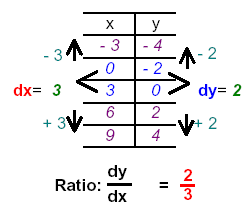
If both the x-intercept and the y-intercept are integers, we can place them in the
middle of the
table. Then we can find the difference in the x-values for dx and the difference in the y-values
for dy and use these differences to build arithmetic sequences for the table.
| Let x = 0, then 2( 0 ) − 3y = 6 or y = -2
which gives the point: ( 0 , -2 )
Let y = 0, then 2x − 3( 0 ) = 6 or x = 3
which gives the point: ( 3 , 0 )
Check the dy and dx on your table. |
 |
Now you must CHECK the top and bottom points in the table to be sure that they are points on
the line:
For the point (- 3, - 4) replace x = - 3 and y = - 4
in the given equation 2x − 3y = 6
CHECK:
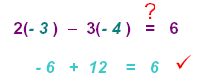
For the point (9, 4) replace x = 9 and y = 4
in the given equation 2x − 3y = 6
CHECK:
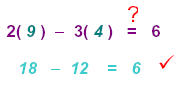
2. For the equation 2x + 5y = 10 complete the two intercept points below.
2x + 5(0) = 10, x = 5 2(0) + 5y = 10, y = 2
( 5 , 0 ) and ( 0 , 2 )
Plot the points and draw the line through the points.. Put the points on the table below, find the
differences dx and dy between the two points. Use these differences to complete the table
of arithmetic sequences. Work in the space below:
Check top and bottom points:
2(- 5) + 5y = 10, y = 4
2(10) + 5y = 10, y = -2
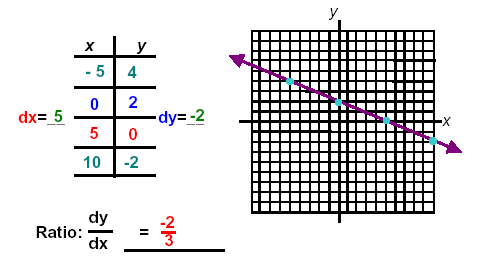
Looking at this line from left to right describe how the points “step†or line “slants†up or down?
Sometimes we encounter a problem where we solve Ax + By = C for y to find intercepts and
neither one is an integer.
3. Graph 3x – 5y = 7. All of the numbers are prime and have no common factors.
Note: If x = 0 then
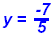 and if y = 0 then and if y = 0 then
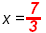 . Points: . Points:
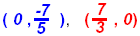
Since neither of these is an integer it will be difficult to use the x-intercept or y-intercept to draw
the graph. We need to find integers as coordinates for the starting point.
If we solve the literal equation for y we get
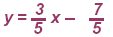
Let us examine the equation
Now, let us again turn to LOGIC: We know that we will get an integer for y if we find a
replacement value for x that will make the sum of the numerators a multiple of 5.
Since - 3 − 7 = -10 we will choose x = -1:
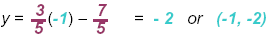
Again, since 12 − 7 = 5 we will choose x = 4:
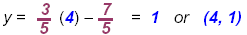
Now we have starting points with integers: ( -1, -2 ) and (4, -1) . We can plot the points then:
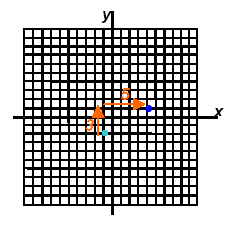 Start at (-1, -2) and note the
move up 3 and right 5
to the next point (4, -1) |
and repeat the move or down 3 -- left 5
find more points and draw the line
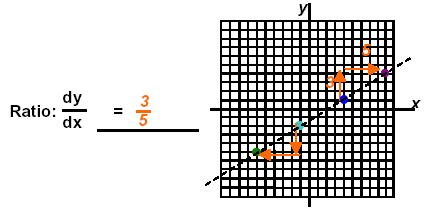
New points ( - 6, - 5 ) ( 9, 4 ) |
|