Prime Factors
To factor a whole number is to write it as a
product of two or more other whole numbers. The individual
numbers in this product are called factors of
the original number.
A prime number or prime is a
whole number which is evenly divisible only by itself and 1. In
other words, prime numbers have only 1 and themselves as factors.
Whether or not the number 1 should be considered a prime number
is a matter of futile debate. Ignoring 1, the first few prime
numbers are:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53,
59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, …
There is no known formula which generates all prime numbers.
Instead, to establish that a number is prime, you have to use a
method of systematic trial and elimination of potential factors
to demonstrate that it has no factors other than itself and 1.
Mathematicians have been intrigued by prime numbers for thousands
of years, and continue to study their properties enthusiastically
today because they have applications in many problems of
technology.
In simplifying fractions, it is useful to begin by factoring
the numerator and denominator into a product of factors which are
all prime numbers – hence the term prime factor
. (We also did this earlier in these notes in attempting to
simplify square roots of numbers.) The procedure is very
straightforward and systematic:
- start by checking for factors of 2 in the number, and
remove as many as possible
- then check for factors of 3 in what’s left after all
factors of 2 have been removed, and remove as many
factors of 3 as possible
- repeat this process on what’s left after previous
prime factors have been removed, using the prime numbers
in turn: 5, 7, 11, 13, … etc. When it is clear that
what’s left to be factored is a prime number itself
(and so cannot be factored further), the process is done.
Example:
Find the prime factors of 156.
Solution:
- 156 is even, so it contains a factor of 2:
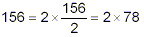
- 78 is even, so it contains a factor of 2:
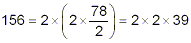
- 39 is not even, so there are no further prime factors of
2. So, check if 39 is divisible by 3. Since 39 / 3 = 13,
a whole number, we conclude that 3 is a prime factor of
39, and so
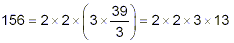
Having removed three prime factors ( 2, 2, and 3) from 156, we
are left with the factor 13. But 13 is itself a prime number.
Thus 156, written as a product of prime factors is
156 = 2 × 2 × 3 × 13
Notice that as we remove prime factors, the number on which we
need to focus further attention is always getting smaller and
smaller.
We’ll do one more really long example to make sure you
clearly understand this systematic approach to determining the
prime factors of a number. Usually however, the numbers we need
to factor are much smaller (hence the factoring process is much
shorter and less tedious) than the one in the next example.
Example:
Find the prime factors of 58212.
Solution:
- 58212 is even, so it contains a factor of 2:
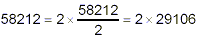
- 29106 is even, so it contains a factor of 2:
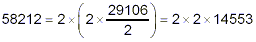
- 14553 is not even, so it does not contain a factor of 2.
But, since 3 divides evenly into 14553, we have that
there is a factor of 3 here:
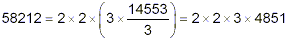
- we are now working on factors of 3. Again, 3 divides
evenly into 4851, so there is at least one more factor of
3:
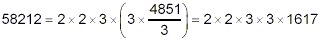
- we are still working on factors of 3. Again, 3 divides
evenly into 1617, so there is at least one more factor of
3:
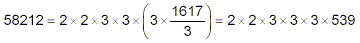
- we are still working on factors of 3. However, a test
calculation shows that 3 does not divide evenly into 539,
so we conclude there are no more factors of 3 in the
original number. Clearly 539 is not divisible by 5. So
the next prime number to try is 7. We find that 539 is
evenly divisible by 7, giving
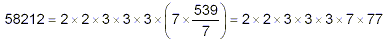
- We can see that the remaining unfactored part, the 77, is
still evenly divisible by 7, so we have:
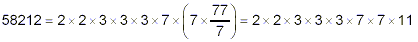
This is the end, because all of the numbers in the product on
the right are prime numbers. Thus, the prime factorization of
58212 is:
58212 = 2 × 2 × 3 × 3 × 3 × 7 × 7 × 11
You can easily verify that multiplying the numbers on the
right together does give 58212, and all seven factors shown are
prime numbers. Thus, this is the requested solution to the
problem.
|