Solving a Quadratic Inequality
A quadratic inequality is a lot like a quadratic equation, except that the equals sign is
replaced by less than (<), greater than (>), less than or equal to ( ) or greater than or
equal to ( ) or greater than or
equal to (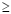 ). For example: ). For example:
4 · x2 - 2
· x + 3
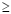 19. 19.
When you solve a quadratic inequality, the idea is to re-arrange the inequality to make x
the subject. Unlike solving an equation, when you solve a quadratic inequality, you can
get one interval of x-values as your solution, or you can get two intervals of x-values as
your solution.
Preliminary Steps in Solving a Quadratic Inequality
When the coefficient of x2 (i.e. the number represented by a) is positive, quadratic
inequalities are much easier to solve if they are in one of the four forms:
a · x2 + b
· x + c > 0
a · x2 + b
· x + c < 0
a · x2 + b
· x + c
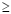 0 0
a · x2 + b
· x + c
 0 0
where b and c are numbers that might be positive, negative or zero. The truly important
things about these forms are:
· One side of the inequality has been reduced to zero.
Before you begin solving the quadratic inequality, it is a good idea to manipulate the
inequality so that that it is one of the four forms listed above.
|