Parent and Family Graphs

Objective

Use a graphing calculator to see how the graphs of quadratic functions change as the coefficients change.

In this lesson, we will start with the parent function y = x ² and study how the graphs change in shape or in position when the coefficients are changed. You should use graphing calculators or computers to graph the families of functions, and try to find similarities and differences between them.

Multiplying x² by a Positive Number

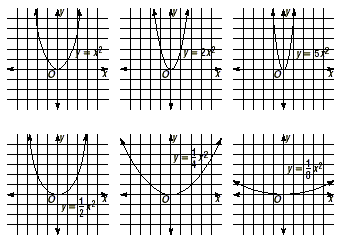
Graph y = x ² and then the following family of functions.

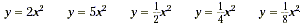
Notice how the sizes of these parabolas change as the coefficient of x ² increases or decreases. Make sure you understand the following characteristics.

1. The vertices and the axes of symmetry of all these parabolas are the same. Namely, the axis of symmetry is the line x = 0, and the coordinates of the vertex are (0, 0). This is because in a quadratic function of the form y = ax ² + 0 x + 0, b = 0, so the axis of symmetry is given by 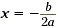or 0, which is the y -axis.

2. The graphs of the quadratic functions y = ax ² , where a > 0, get more narrow as the value of a increases. The graphs get wider as the value of a decreases.

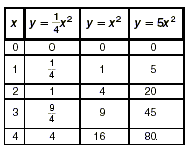
Why do parabolas change sizes in this way? The larger the value of a in y = ax ² , the faster the y variable increases as x grows. To see this, make a table of values of the functions 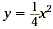, y = x ² , and y = 5 x ² . It is clear from this table that the larger the coefficient of x ² , the faster the y value grows. This results in a steeper incline of the graph, or a “narrower” parabola. Similarly, the smaller the coefficient of x ² , the more slowly the y value grows. This results in a more gradual incline of the graph, or a “wider” parabola.

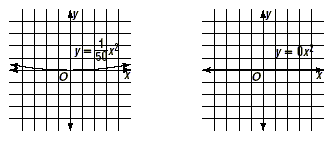
What happens as the coefficient a in y = ax ² gets smaller and smaller (but remains positive), until it approaches 0? As a approaches 0, the parabolas get wider and wider until they approach a flat line, namely the graph of y = 0x or 0, which is the x-axis.

Multiplying x ² by a Negative Number

Now what happens to the graphs of y = ax ² when a is negative? Graph the following family of functions.

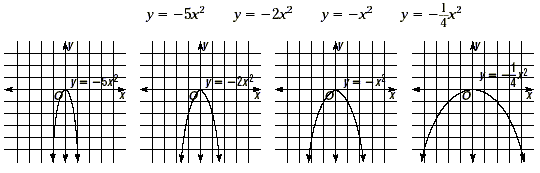
When the a is negative in y = ax ² , the parabolas open downwards. This is because as x grows, the y variable becomes more and more negative. So the graphs incline downward. Notice that these graphs have the same characteristics that we saw before.

1. These parabolas all have the same axes of symmetry and vertices. The axis of symmetry is still the vertical line x = 0 (or the y -axis), and the vertices are still at (0, 0). This is because in these functions y = - ax ² + 0x + 0, or 0. Notice however that the vertices are now maximum points of the graphs, where in the earlier examples they were minimum points.

2. Similar to previous examples, as the coefficient a in y = ax ² becomes smaller (more negative), the parabola becomes more narrow. As a gets closer to zero, the parabola gets wider. This is because the smaller the coefficient a is, the faster the y value decreases (gets more negative) as the x value grows. Have your students make tables of values of the functions graphed above to verify this.